A block of mass 4m is attached to a vertical spring of spring constant k. The block is made by gluing two blocks of mass 3m and m, respectively. Initially, the block is in equilibrium and at rest (Fig. 15.13a). At t=0, the part of the block having ass 3m falls down. Considering hanging point on ceiling as y=0 and downward direction as positive y, find y-coordinate of mass m as a function of time.
(1) As the original block of mass 4m is in equilibrium, the combined mass will be stretching the spring by 4mg/k. Thus, the spring will be 4mg/k below the natural length. As the bigger block falls, the smaller block will experience a force larger than its weight in upward direction.
(2) The block remaining attached to the spring will be undergoing SHM. To find equation of SHM, we need to find angular frequency, amplitude, and initial phase
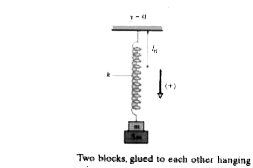
Calculations: When the extension in the spring is x, the net force on the block is
mg−kx=md2xdt2
Again as x= 0 is not position of equilibrium, we have to shift origin to the position of equilibrium.
Defining x=(mg/k)+s, as at s=0, x = mg/k is the position of equilibrium. Substituting for x in the equation we get
mg−k(mgk+s)=md2sdt2
On solving we get,
d2sdt2=−(km)s
s=xmsin(ωt+ϕ) (with ω=√km)
Now we have to find xm. We have defined xm as distance between v=0 and a=0. At t=0, the block was at rest with extension of spring being 4mg/k and at the new equilibrium position extension of spring is mg/k.
Thus, xm=3mgk
Now we have to find the initial phase. As the particle is at rest at t=0 on positive side, the initial phase will be π/2.
ϕ=π2
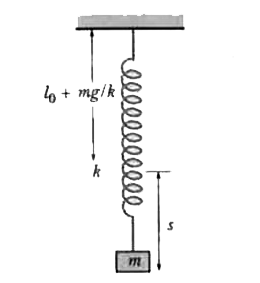
Thus, the y coordinate of the block
y=l0+mgk+s
Substituting, all the values from above, we get
y=l0+mgk+3mgksin[√kmt+π2]
Note: At time t=0, the distance of the block from the ceiling is l0+4mg/k, which can be verified by putting t=0 in the above equation.
Topper's Solved these Questions
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Checkpoint
8 Videos
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Problems
39 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)
10 Videos
- PHOTONS AND MATTER WAVESBOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)
4 Videos
Similar Questions
Knowledge Check

A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will beAx√m2kBx√2kmCxmkDx2km
A block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will be
View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionIn the figure all spring are identical having spring constant k and mass m each The block also mass m The frequency of oscillation of the block is
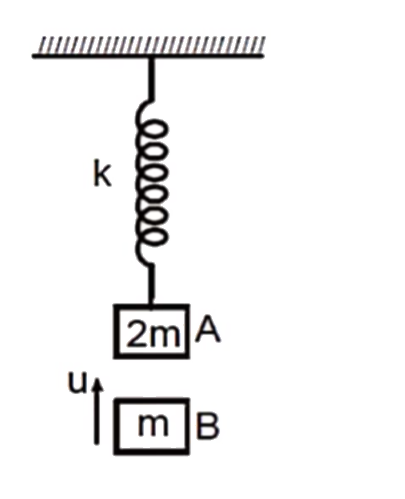
View SolutionA block A of mass 2m is hanging from a vertical massless spring of spring constant k and is in equilibrium. Another block B of mass m strikes the block A with velocity u and sticks to it as shown in the figure. The magnitude of the acceleration of the combined system of the blocks just after the collision is
View Solution
