Figure 15-24 gives the one-dimensional potential energy well for a 4.0kg particle (the function U (x) has the form bx2 and the vertical axis scale is set by U= 2.0 J). (a) If the particle passes through the equilibrium position with a velocity of 85 cm/s, will it be turned back before it reaches x= 15cm? (b) If yes, at what position, and if no, what is the speed of the particle at x= 15cm?
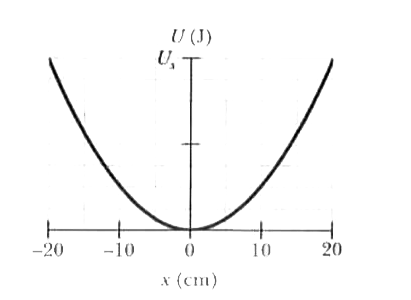
(a) 15cm, (b) 0.40m/s
Topper's Solved these Questions
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions
57 Videos
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Checkpoint
8 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)
10 Videos
- PHOTONS AND MATTER WAVESBOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)
4 Videos
Similar Questions
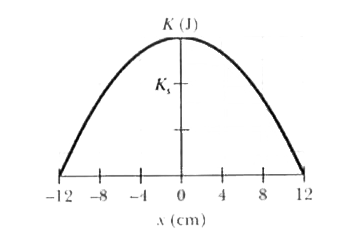
Figure 15.39 shows the kinetic energy K of a simple harmonic oscillator versus its position x. The vertical axis scale is set by Ks=8.0J. What is the spring constant?
View SolutionThe potential energy U(x) of a particle moving along x - axis is given by U(x)=ax−bx2. Find the equilibrium position of particle.
View Solution
Knowledge Check
The potential energy of a particle oscillating on x-axis is given as U+20+(x−2)2. The mean position is at
Ax=2mBx=1mCx=3mDx=4mThe potential energy of a particle in a certain field has the form U=a/r2−b/r, where a and b are positive constants, r is the distance from the centre of the field. Find:
(a) the value of r0 corresponding to the equilibrium position of the particle, examine where this position is steady,
(b) the maximum magnitude of the attraction force, draw the plots U(r) and Fr(r) (the projections of the force on the radius vector r).A2abB2abC−abDabPotential energy of a particle at position x is given by U=(x2−4x)J. Which of the following is equilibrium position of the particle?
Ax=0Bx=5mCx=2mDx=4m
The potential energy U(x) of a particle moving along x - axis is given by U(x)=ax−bx2. Find the equilibrium position of particle.
View SolutionPotential energy of a particle at position x is given by U=(x2−4x)J. Which of the following is equilibrium position of the particle?
View SolutionThe potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
View SolutionThe potential energy of 1 kg particle is [U(x)=(0.25x4)−(0.5x2)] J If total mechanical energy is 2 J, then maximum KE is
View SolutionThe potential energy of 1 kg particle is [U(x)=(0.25x4−0.5x2)J] If total mechanical energy is 2 J, then maximum K.E. is
View Solution
