Two particles oscillate in simple harmonic motion along a common straight-line segment of length A. Each particle has a period of 1.5s but they differ in phase by π/6 rad. (a) How far apart are they (in terms of A) 0.60s after the lagging particle leaves one end of the path? (b) Are they then moving in the same direction, toward each other, or away from each other?
(a) ~~0.093A, (b) Moving in the same direction.
Topper's Solved these Questions
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions
57 Videos
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Checkpoint
8 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)
10 Videos
- PHOTONS AND MATTER WAVESBOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)
4 Videos
Similar Questions
Two particles perform linear simple harmonic motion along the same path of length 2 A and period T as shown in the graph below. The phase difference between them is
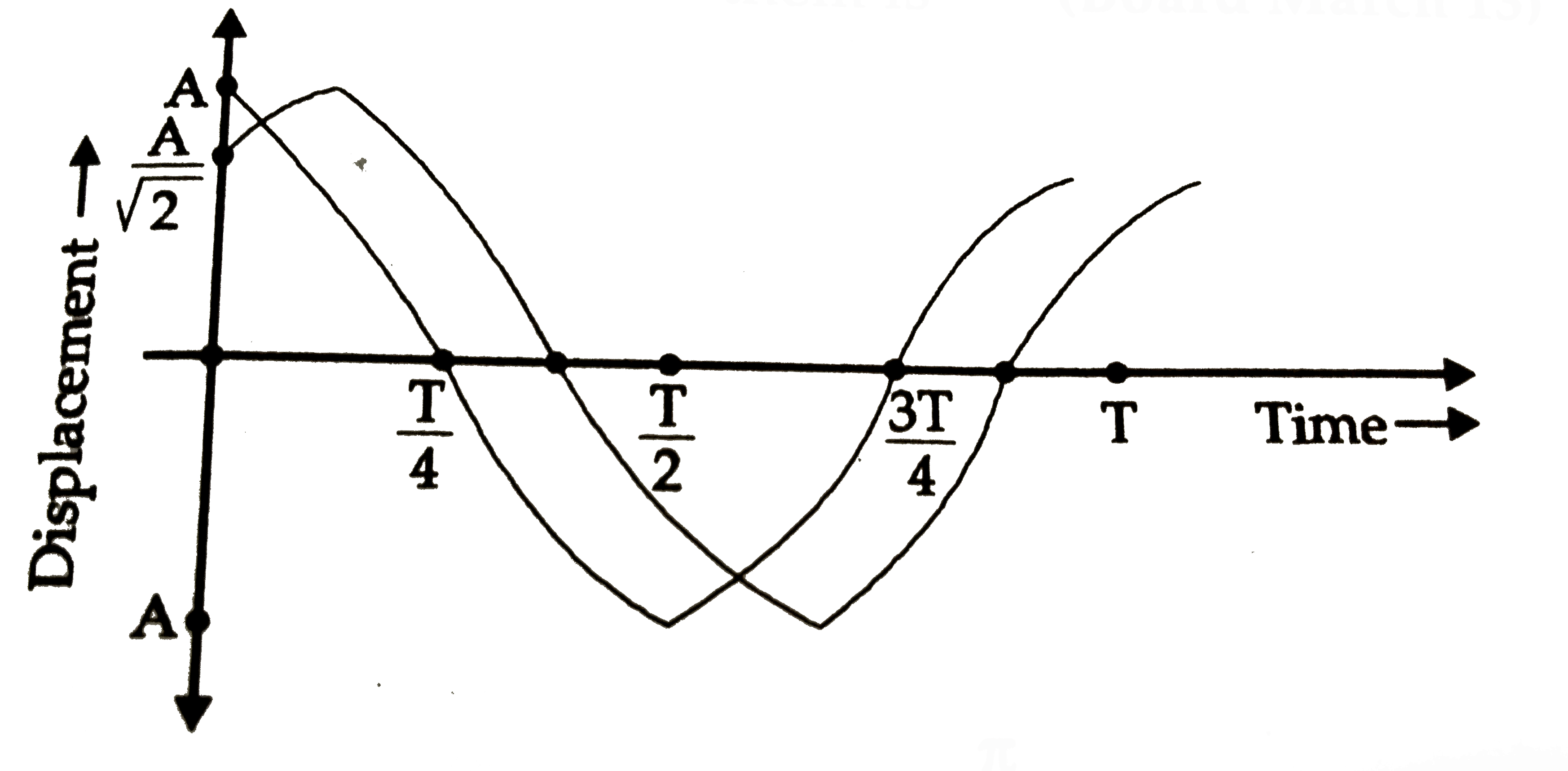
View SolutionTwo particles start oscillating together in shm along the same straight line. Their periods are 2 s and 4 s. What is their phase difference afterls from the start?
View Solution
Knowledge Check
A particle moves with simple harmonic motion in a straight line. In first τs, after starting form rest it travels a destance a, and in next τs it travels 2a, in same direction, then:
A(a)amplitude of motion is 3a.B(b) time period of oscllations is 8τ.C(c ) amplitude of motion is 4τ.D(d) time period of oscillations is 6τ.Two particles undergo SHM along the same line with the same time period (T) and equal amplitude (A). At a particular instant one particle is at x=−A and the other is at x = 0. They move in the same direction. They will cross each other at
 At = 4T/3Bt = 3T/8Cx = A/2Dx=A/√2
At = 4T/3Bt = 3T/8Cx = A/2Dx=A/√2Time period (T) and amplitude (A) are same for two particle which undergoes SHM along the same line. At one particular instant one particle is at phase3π2and the other is at zero, while moving in the same direction. Find the time at which they will cross each other
A4T/2B3T/8C3T/4D3T/7
A particle moves with simple harmonic motion in a straight line. In first τs, after starting form rest it travels a destance a, and in next τs it travels 2a, in same direction, then:
View SolutionThe composition of two simple harmonic motions of equal periods at right angle to each other and with a phase difference of π results in the displacement of the particle along
View SolutionThe composition of two simple harmonic motions of equal periods at right angle to each other and with a phase difference of p results in the displacement of the particle along
View SolutionTwo particles are executing SHM in a straight line. Amplitude A and the time period T of both the particles are equal. At time t=0, one particle is at displacement x1=+A and the other x2=(−A2) and they are approaching towards each other. After what time they across each other? T4
View SolutionThe composition of two simple harmonic motions of equal periods at right angle to each other and with a phase difference of π result in the displacement of the particle along
View Solution
