In Fig. 15.26, the pendulum consists of a uniform disk with radius r= 10.0cm and mass 500g attached to a uniform rod with length L = 500mm and mass 250g. (a) Calculate the rotational inertia of the pendulum about the pivot point. (b) What is the distance between the pivot point and the center of mass of the pendulum? (c ) Calculate the period of oscillation.
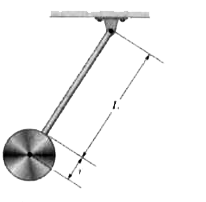
(a) 0.203kg.M2, (b) 0.483m, (c ) 1.50s
Topper's Solved these Questions
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions
57 Videos
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Checkpoint
8 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)
10 Videos
- PHOTONS AND MATTER WAVESBOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)
4 Videos
Similar Questions
A uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?
View SolutionA uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?
View Solution
Knowledge Check
A pendulum is formed by pivoting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown.
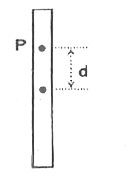
The time period of this pendulum when d = L/2 will beA2π√2l3gB2π√3l2gC4π√l3gD2π3√2lgA pendulum is formed by pivotting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown.

The time period of this pendulum when d = L/2 will beA2π√2l3gB2π√3l2gC4π√l3gD2π3√2lg
In Fig 15.19a, a meter stick swings about a pivot point at one end, at distance h from the stick's center of mass.
What is the distance L0 between the pivot point O of the stick and the center of oscillation of the stick?
View SolutionIn Fig 15.19a, a meter stick swings about a pivot point at one end, at distance h from the stick's center of mass.
What is the period of oscillation T?
View SolutionA conical pendulum, a thin uniform rod of length l and mass m, rotates uniformly about a vertical axis with angular velocity ω(the upper end of the rod is hinged). Find the angle θ between the rod and the vertical.
View SolutionFigure shows a thin, uniform rod of mass M and length L, on an x axis with the origin at the rod's center.
(a) What is the rotational inertia of the rod about the perpendicular rotation axis through the center?
(b) What is the rod's rotational inertia I about a new rotation axis that is perpendicular to the rod and through the left end?
View SolutionTwo uniform solid of masses m1 and m2 and radii r1 and r2 respectively, are connected at the ends of a uniform rod of length l and mass m. Find the moment of inertia of the system about an axis perpendicular to the rod and passing through a point at a distance of a from the centre of mass of the rod as shown in figure.

View SolutionTwo uniform solid of masses m1 and m2 and radii r1 and r2 respectively, are connected at the ends of a uniform rod of length l and mass m. Find the moment of inertia of the system about an axis perpendicular to the rod and passing through a point at a distance of a from the centre of mass of the rod as shown in figure.

View Solution
