If the phase angle for a block -spring system in SHM is π/8 rad and the block's position is given by x=xmcos(ωt+ϕ), what is the ratio of the kinetic energy to the potential energy at time t= 0?
The correct Answer is:0.172
To find the ratio of kinetic energy (KE) to potential energy (PE) for a block-spring system in simple harmonic motion (SHM) at time t=0, we will follow these steps:
Step 1: Write the expressions for kinetic energy and potential energy
The kinetic energy KE in SHM is given by the formula:
KE=12mv2
where v is the velocity of the block.
The potential energy PE in SHM is given by the formula:
PE=12kx2
where x is the displacement of the block from the equilibrium position.
Step 2: Determine the expressions for velocity and displacement at t=0
The position of the block is given by:
x=xmcos(ωt+ϕ)
At t=0:
x=xmcos(ϕ)
Substituting ϕ=π8:
x=xmcos(π8)
The velocity v can be found by differentiating the position with respect to time:
v=dxdt=−xmωsin(ωt+ϕ)
At t=0:
v=−xmωsin(ϕ)=−xmωsin(π8)
Step 3: Substitute values into the kinetic and potential energy formulas
Now we can substitute the values of x and v into the formulas for kinetic and potential energy.
1. Kinetic Energy at t=0:
KE=12m(−xmωsin(π8))2=12mx2mω2sin2(π8)
2. Potential Energy at t=0:
PE=12k(xmcos(π8))2=12kx2mcos2(π8)
Step 4: Find the ratio of kinetic energy to potential energy
Now we can find the ratio KEPE:
KEPE=12mx2mω2sin2(π8)12kx2mcos2(π8)
Canceling 12 and x2m:
KEPE=mω2sin2(π8)kcos2(π8)
Step 5: Substitute ω2 using ω=√km
Substituting ω2=km:
KEPE=m(km)sin2(π8)kcos2(π8)=sin2(π8)cos2(π8)=tan2(π8)
Step 6: Calculate the value of tan2(π8)
Using a calculator or trigonometric tables, we find:
tan(π8)≈0.414
Thus:
tan2(π8)≈(0.414)2≈0.171
Final Answer
The ratio of kinetic energy to potential energy at t=0 is approximately:
KEPE≈0.171
KE=12mv2
where v is the velocity of the block.
PE=12kx2
where x is the displacement of the block from the equilibrium position.
x=xmcos(ωt+ϕ)
At t=0:
x=xmcos(ϕ)
Substituting ϕ=π8:
x=xmcos(π8)
v=dxdt=−xmωsin(ωt+ϕ)
At t=0:
v=−xmωsin(ϕ)=−xmωsin(π8)
KE=12m(−xmωsin(π8))2=12mx2mω2sin2(π8)
PE=12k(xmcos(π8))2=12kx2mcos2(π8)
KEPE=12mx2mω2sin2(π8)12kx2mcos2(π8)
Canceling 12 and x2m:
KEPE=mω2sin2(π8)kcos2(π8)
KEPE=m(km)sin2(π8)kcos2(π8)=sin2(π8)cos2(π8)=tan2(π8)
tan(π8)≈0.414
Thus:
tan2(π8)≈(0.414)2≈0.171
The ratio of kinetic energy to potential energy at t=0 is approximately:
KEPE≈0.171
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions57videos
OSCILLATIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Checkpoint8videos
OSCILLATIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)10videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)4videos
PHOTONS AND MATTER WAVES
Similar Questions
A mass of 1 kg is executing SHM which is give by, x=6.0cos(100t+π/4)cm. What is the maximum kinetic energy?
View SolutionIf the position of the block in a block-spring oscillator is given by
x(t)=(3.00×10−3m)cos[(4.00rad/s)t+0.120rad], what is the block's position, velocity and acceleration at time t= 2.30s?View Solution
Knowledge Check
- Question 1 - Select One
If x=Asin(ωt+π6), then find the minimum time t when kinetic energy of SHM is same as its potential energy.
AπωB2πωCπ6ωDπ12ω - Question 2 - Select One
In S.H.M., the graph between kinetic energy K and time 't' is
A B
B C
C D
D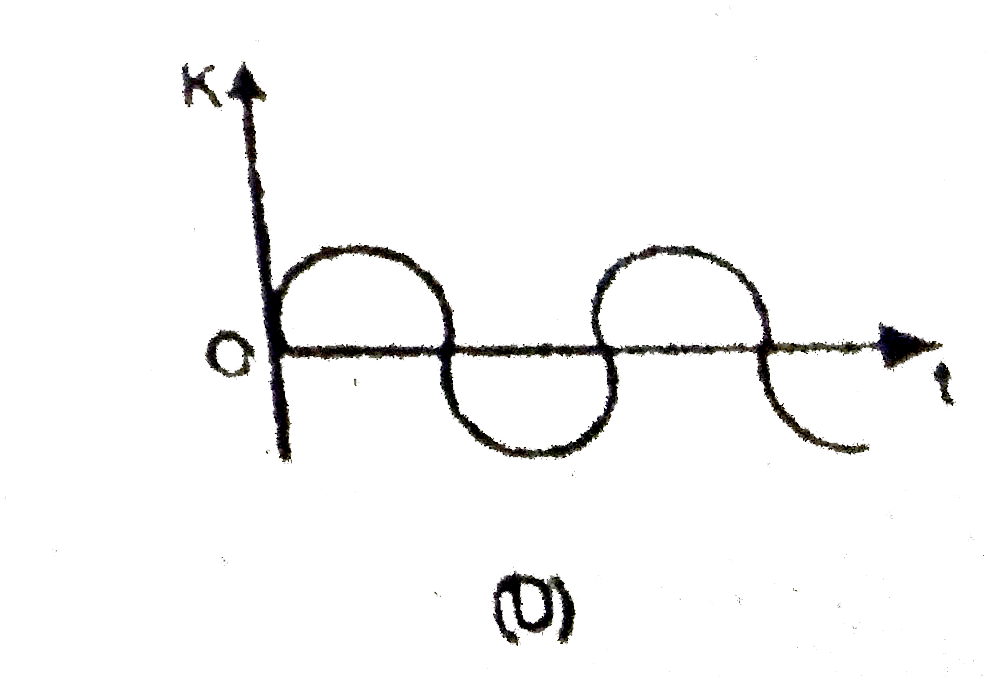
- Question 3 - Select One
A simple pendulum is oscillating with amplitude 'A' and angular frequency 'ω' . At displacement 'x' from mean position, the ratio of kinetic energy to potential energy is
Ax2A2−x2Bx2−A2x2CA2−x2x2DA−xx
A 1.0 kg block is initially at rest on a horizontal frictionless surface when a horizontal force along an x axis is applied to the block. The force is given by →F(x)=(2.5−x2)ˆiN, where x is in meters and the initial position of the block is x=0. (a) What is the kinetic energy of the block as it passes through x=2.0m ? (b) What is the maximum kinetic energy of the block between x=0 and x=2.0m ?
View SolutionA particle undergoing simle harmonic motion has time dependent displacement given by x(t)=Asin(πt)90.The ratio of kinetic to potential energy of this partle at t= 210s will be :
View SolutionFor a particle executing S.H.M., the kinetic energy K is given K=K0cos2ωt. The maximum value of potential energy is:
View SolutionAssertion : x-t equation of a particle in SHM is given as :x=Acosωt
Reason : In the given equation the minimum potential energy is zero.View SolutionA block whose mass is 1 kg is fastened to a spring. The spring has a spring constant of 100N/m. the block is pulled to a distance x=10 cm from its equilibrium position at x=0 on a frictionless surface from rest at t=0. the kinetic energy and potential energy of the block when it is 5 cm away from the mean position is
View Solution

