A thin uniform rod (mass= 0.90kg) swings about an axis that passes through one end of the rod and is perpendicular to the plane of the swing. The rod swings with a period of 1.5s and an angular amplitude of 10∘. (a) What is the length of the rod? (b) What is the maximum kinetic energy of the rod as it swings?
(a) 0.84m, (b) 0.056J
Topper's Solved these Questions
- OSCILLATIONSBook:RESNICK AND HALLIDAYChapter:OSCILLATIONSExercise:Practice Questions
Explore 57 Videos
- OSCILLATIONSBook:RESNICK AND HALLIDAYChapter:OSCILLATIONSExercise:Checkpoint
Explore 8 Videos
- MOTION IN TWO AND THREE DIMENSIONSBook:RESNICK AND HALLIDAYChapter:MOTION IN TWO AND THREE DIMENSIONSExercise:PRACTICE QUESTIONS (MATRIX-MATCH)
Explore 10 Videos
- PHOTONS AND MATTER WAVESBook:RESNICK AND HALLIDAYChapter:PHOTONS AND MATTER WAVESExercise:PRACTICE QUESTIONS(Integer Type)
Explore 4 Videos
Similar Questions
Moment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
View SolutionCalculate the moment of inertia of a uniform rod of mass M and length l about an axis passing through an end and perpendicular to the rod. The rod can be divided into a number of mass elements along the length of the rod.
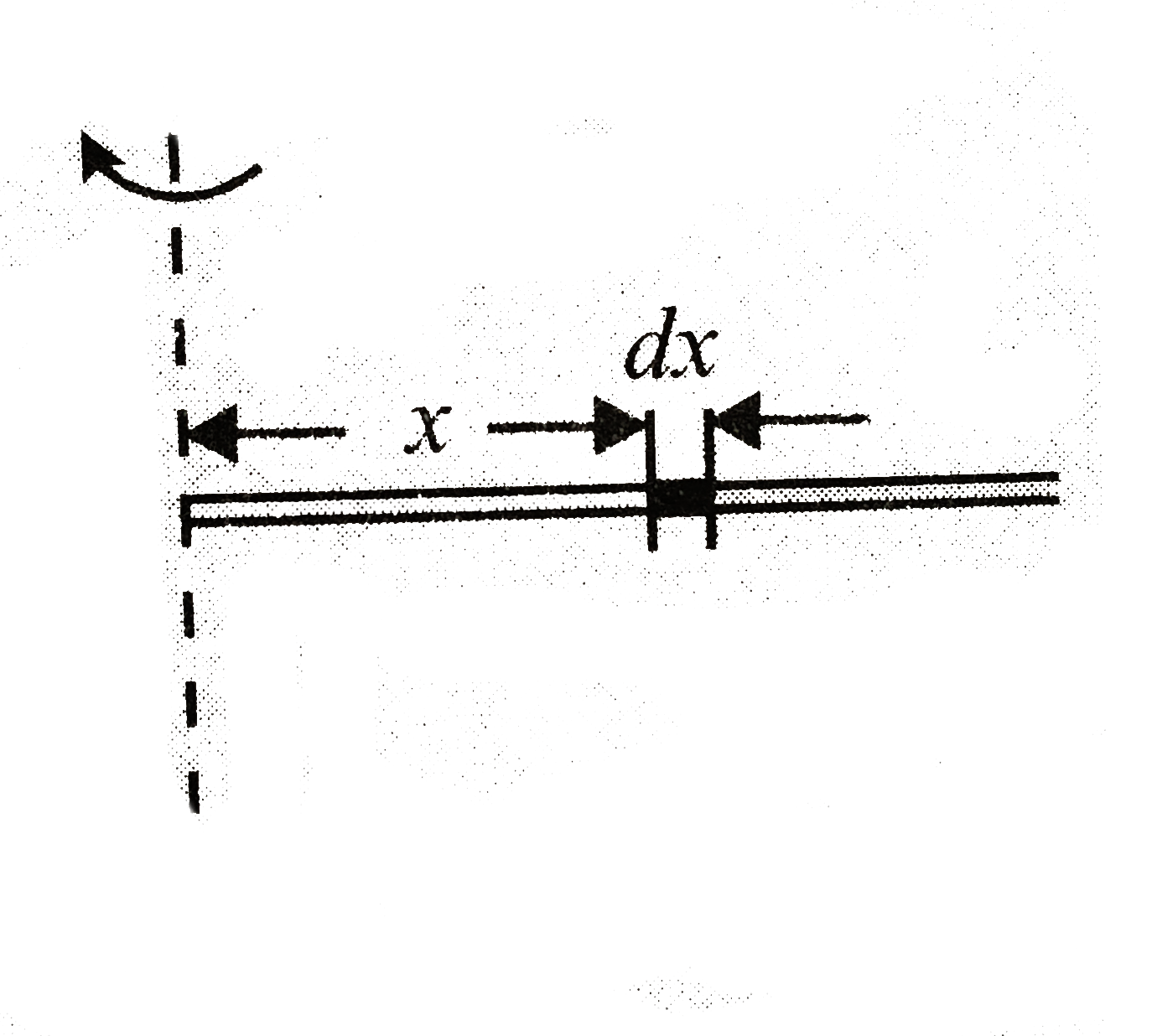
View Solution
Knowledge Check
The radius of gyration of an uniform rod of length l about an axis passing through one of its ends and perpendicular to its length is.
Al√2Bl3Cl√3Dl2The radius of gyration of a uniform rod of length l about an axis passing through one of its ends and perpendicular to its length is
Al√2Bl3Cl√3Dl2Moment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
Aml212Bml23C7ml248Dml29
Calculate the moment of inertia of a uniform rod of mass M and length l about an axis passing through an end and perpendicular to the rod. The rod can be divided into a number of mass elements along the length of the rod.
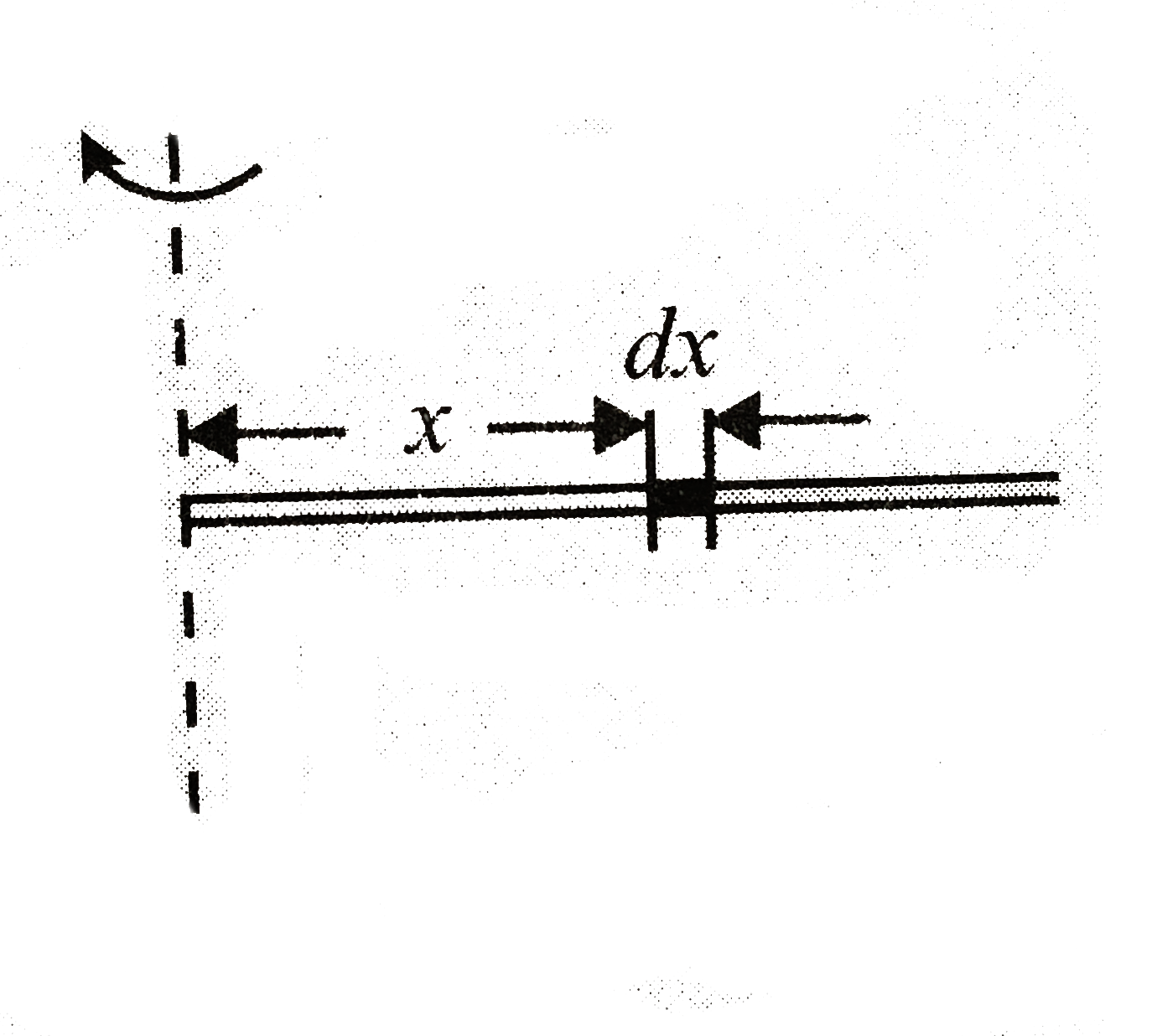
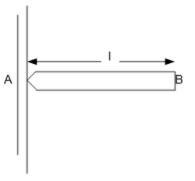
View SolutionA uniform rod AB of length l and mass m is free to rotate about an Axis passing through A and perpendicular to length of the rod. The rod is released from rest as shown in figure. Given that the moment of inertia of the rod about A is ml23 The initial angular acceleration of the rod will be
View SolutionA uniform rod of mass 300 g and length 50 cm rotates at a uniform angular speed of 2 rad/s about an axis perpendicular to the rod through an end. Calculate a. the angular momentum of the rod about the axis of rotation b. the speed of the centre of the rod and c. its kinetic energy.
View SolutionMoment of inertia of a thin uniform rod about an axis passing through one end perpendicular to its length is I . Then moment of inertia the same rod about the central axis perpendicular to its plane is
View SolutionLet M be the mass and L be the length of a thin uniform rod. In first case, axis of rotation is passing through centre and perpendicular to the length of the rod. In second case, axis of rotation is passing through one end and perpendicular to the length of the rod. The ratio of radius of gyration in first case to second case is
View Solution
