What is the phase constant for the harmonic oscillator with the velocity function v(t) given in Fig. 15.34 if the position function x(t) has the form x=xmcos(ωt+ϕ)? The vertical axis scale is set by vx=8.0cm/s.
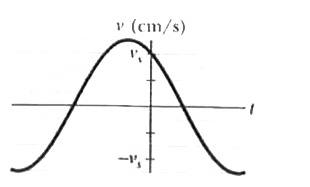
−0.927rad or +5.36 rad
Topper's Solved these Questions
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions
57 Videos
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Checkpoint
8 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)
10 Videos
- PHOTONS AND MATTER WAVESBOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)
4 Videos
Similar Questions
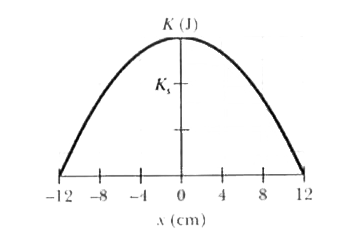
Figure 15.39 shows the kinetic energy K of a simple harmonic oscillator versus its position x. The vertical axis scale is set by Ks=8.0J. What is the spring constant?
View SolutionA sinusoidal transverse wave of wavelength 18 cm travels along a string in the positive direction of an x axis. The displacement y of the string particle at x= 0) is given in Fig. 16-41 as a function of time t. The scale of the vertical axis is set by y1=4.0cm, The wave equation is to be in the form y(x,t)=ynIsin(kx±ωt+ϕ). (a) At t= 0), is a plot of y versus x in the shape of a positive sine function on a legative sinc function? What are (b)ynI(c)k,(d)ω(e)ϕ, (f) the sign in front of ω, and (g) the speed of the wave? (h) What is the transverse velocity of the particle at x=0 when t=5.0 s?
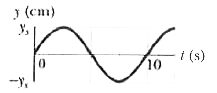
View Solution
Knowledge Check
The displacement of a simple harmonic oscillator is given by x = 4 cos (2πt+π/4)m. Then velocity of the oscillator at t = 2 s is
A4π√2m/sB4π√2m/sC√2π4m/sD4√2πm/sThe equation of displacement of a harmonic oscillator is x =3sinωt+4 cosωtamplitude is
A2B5C7D12If a particle is moving the velocity v(t)=cos πt, along a straight line such that at t=0, s=4, its position function is given by
A1πcosπt+2B−1πsinπt+4C1πsinπt+4Dnone of these
If the phase angle for a block -spring system in SHM is π/8 rad and the block's position is given by x=xmcos(ωt+ϕ), what is the ratio of the kinetic energy to the potential energy at time t= 0?
View SolutionIf velocity is given by following function V = x2 . Then find out relation between x & t (assume x = 1 m at t = 0)
View SolutionAcceleration of particle moving along the x-axis varies according to the law a=−2v, where a is in m/s2 and v is in m/s. At the instant t=0, the particle passes the origin with a velocity of 2m/s moving in the positive x-direction.
(a) Find its velocity v as function of time t.
(b) Find its position x as function of time t.
(c) Find its velocity v as function of its position coordinates.
(d) find the maximum distance it can go away from the origin.
(e) Will it reach the above-mentioned maximum distance?
View SolutionAcceleration of particle moving along the x-axis varies according to the law a=−2v, where a is in m/s2 and v is in m/s. At the instant t=0, the particle passes the origin with a velocity of 2m/s moving in the positive x-direction.
(a) Find its velocity v as function of time t.
(b) Find its position x as function of time t.
(c) Find its velocity v as function of its position coordinates.
(d) find the maximum distance it can go away from the origin.
(e) Will it reach the above-mentioned maximum distance?
View SolutionA particle performs harmonic oscillations along the x axis about the equilibrium position x=0. The oscillation frequency is ω=4.00s−1. At a certain moment of time the particle has a coordinatex0=25.0cm and its velocity is equal to vx0=100cm/s.
Find the coordinate x and the velocity vx of the particle t=2.40s after that moment.
View Solution
