In Fig. , the two light waves that are represented by the rays have wavelength 550.0 nm before entering media 1 and 2. They also have equal amplitudes and are in phase. Medium 1 is now just air, and medium 2 is a transparent plastic layer of index of refraction 1.600 and thickness 2.600 μm.
If the waves reached the same point on a distant screen, what type of interference would they produce?
Reasoning: We need to compare the effective phase difference of the waves with the phase differences that give the extreme types of interference. Here the effective phase difference of 0.84 wavelength is between 0.5 wavelength (for fully destructive interference, or the darkest possible result) and 1.0 wavelength (for fully constructive interference, or the brightest possible result), but closer to 1.0 wavelength. Thus, the waves would produce intermediate interference that is closer to fully constructive interference - they would produce a relatively bright spot.
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - CHECKPOINT
6 Videos
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PROBLEMS
61 Videos
- HYDROGEN ATOMBOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS(Integer Type)
6 Videos
- MAGNETIC FIELDS DUE TO CURRENTSBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)
4 Videos
Similar Questions
In Fig. , the two light waves that are represented by the rays have wavelength 550.0 nm before entering media 1 and 2. They also have equal amplitudes and are in phase. Medium 1 is now just air, and medium 2 is a transparent plastic layer of index of refraction 1.600 and thickness 2.600 μm.
What is the phase difference of the emerging waves in wavelengths, radians, and degrees? What is their effective phase difference (in wavelengths)?
View SolutionLight of wavelength 6000Å in air enters a medium of refractive index 1.5. What will be its wavelength in the medium ?
View Solution
Knowledge Check
An e.m. wave is travelling through a medium of refractive index μ1, and is incident on the boundary of a medium of refractive index μ2. IF the wave reflects at the boundary
AThe wave undergoes a phase change of 180∘ if μ1<μ2BThe wave undergoes a phase change of 180∘ if μ1>μ2CThe wave undergoes a phase change if μ1<μ2DThe wave undergoes a phase change if μ1>μ2A ray of light is incident obliquely on medium 1 and then passes through two media namely 2 and 3 before emerging into medium 1 again.
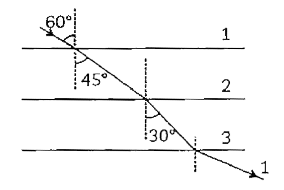
The refractive index of medium 3 respect to medium 1 is:A12B√32C1√2D√3A ray of light passes from solid medium 1 into solid medium 2. The refractive index of medium 1 is the same as that of medium 2. Which of the figures correctly shows the path of the ray of light in the two mediums?
A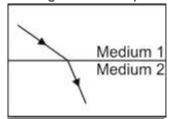 B
B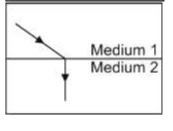 C
C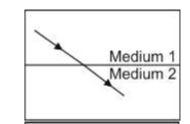 D
D
What happens to the frequency, wavelength and speed of light that crosses from a medium with index of refraction μ1 to one with index of refraction μ2?
View SolutionWhat happens to the frequency, wavelength and speed of light that crosses from a medium with index of refraction μ1 to one with index of refraction μ2?
View SolutionAssume that two waves of light in air, of wavelength 585 nm, are initially in phase. One travels through a glass layer of index of refraction n1=160 and thickness L. The other travels through an equally thick plastic layer of index of refraction n2=1.50. (a) What is the smallest value L should have if the waves are to end up with a phase difference of 5.65 rad? (b) If the waves arrive at some common point with the same amplitude, is their interference fully constructive, fully destructive, intermediate but closer to fully constructive, or intermediate but closer to fully destructive?
View SolutionTwo light waves having the same wavelength λ in vacuum are in phase initially. Then the first ray travels a path of length L1 through a medium of refractive index μ1. Then second ray travels a path of length L2 throug a medium of refractive index μ2. The two waves are then combined to observed interference effects. The phase difference between the two, when they interfere, is
View SolutionA light wave in air enters a medium of refractive index 43. If the wavelength of light in air is 6000Å, then the wave number of light in the medium is
View Solution
