White light is used to illuminate the two slits in Young's experiment. The separation between the slits is d and the screen is at a distance D(»d) from the slits. At a point directly in front of one of the slits, certain wavelength is missing. The missing wavelength
λ=d2/D
λ=d2/5D
λ=d2/3D
All of these
The correct Answer is:D
To find the missing wavelength in Young's double-slit experiment when white light is used, we can follow these steps:
1. Understanding the Setup:
- In Young's experiment, two slits are separated by a distance d, and a screen is placed at a distance D from the slits. The distance D is much larger than d.
2. Identifying the Point of Interest:
- We are interested in a point directly in front of one of the slits. At this point, we need to find the condition for destructive interference (a dark fringe).
3. Calculating Path Difference:
- The path difference (Δx) between the light waves coming from the two slits at this point is given by:
Δx=d⋅yD
- Here, y is the vertical distance from the midpoint between the slits to the point on the screen. Since we are directly in front of one of the slits, y is effectively 0, but we need to consider the distance from the midpoint to the screen, which is D/2.
4. Substituting Values:
- Therefore, substituting y=D/2 into the path difference formula gives:
Δx=d⋅(D/2)D=d2
5. Condition for Destructive Interference:
- For a dark fringe (minimum), the path difference must satisfy the condition:
Δx=(m+12)λ
- Here, m is an integer (0, 1, 2, ...), and λ is the wavelength of light.
6. Setting Up the Equation:
- Setting the path difference equal to the condition for minima:
d2=(m+12)λ
7. Solving for Wavelength:
- Rearranging this gives:
λ=d2(m+12)
- For m=0:
λ=d2⋅12=d1=d
- For m=1:
λ=d2⋅32=d3
- For m=2:
λ=d2⋅52=d5
8. Conclusion:
- The missing wavelengths are d, d3, and d5. Thus, the answer is that the missing wavelength can be any of these values.
- In Young's experiment, two slits are separated by a distance d, and a screen is placed at a distance D from the slits. The distance D is much larger than d.
- We are interested in a point directly in front of one of the slits. At this point, we need to find the condition for destructive interference (a dark fringe).
- The path difference (Δx) between the light waves coming from the two slits at this point is given by:
Δx=d⋅yD
- Here, y is the vertical distance from the midpoint between the slits to the point on the screen. Since we are directly in front of one of the slits, y is effectively 0, but we need to consider the distance from the midpoint to the screen, which is D/2.
- Therefore, substituting y=D/2 into the path difference formula gives:
Δx=d⋅(D/2)D=d2
- For a dark fringe (minimum), the path difference must satisfy the condition:
Δx=(m+12)λ
- Here, m is an integer (0, 1, 2, ...), and λ is the wavelength of light.
- Setting the path difference equal to the condition for minima:
d2=(m+12)λ
- Rearranging this gives:
λ=d2(m+12)
- For m=0:
λ=d2⋅12=d1=d
- For m=1:
λ=d2⋅32=d3
- For m=2:
λ=d2⋅52=d5
- The missing wavelengths are d, d3, and d5. Thus, the answer is that the missing wavelength can be any of these values.
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
23 Videos
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (Linked Comprehension)
21 Videos
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PROBLEMS
61 Videos
- HYDROGEN ATOMBOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS(Integer Type)
6 Videos
- MAGNETIC FIELDS DUE TO CURRENTSBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)
4 Videos
Similar Questions
At a point on the screen directly in front of one of the slits, find the missing wavelengths.
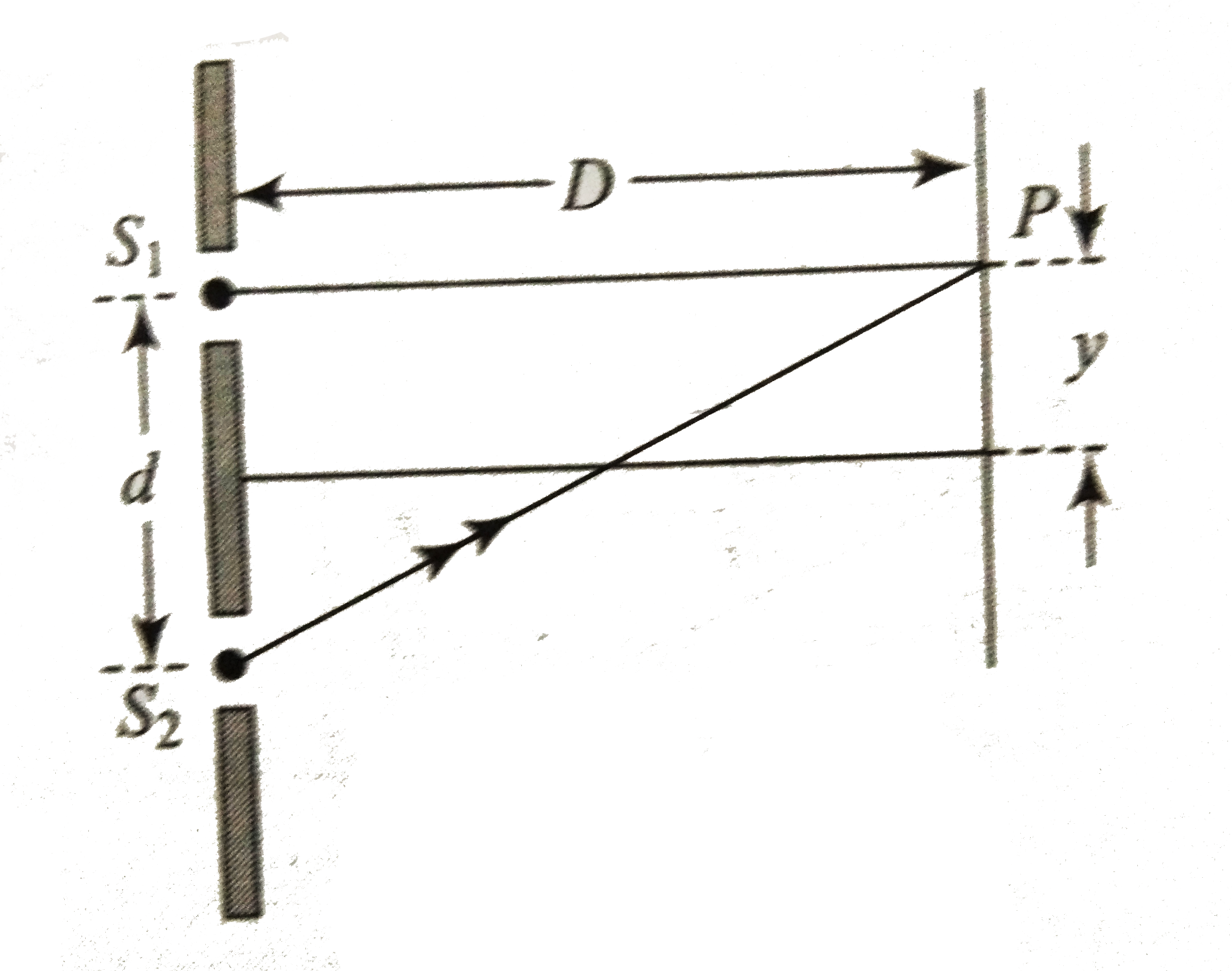
View SolutionWhite light is used to illuminate the two slits in Young's double slit experiment. The separation between the slits is b and the screen is at a distance D>>b from slits. At a point on the screen directly in front of one of the slits, the missing wavelengths are
View Solution
Knowledge Check
White light is used to illuminate the two slits in a Young's double slit experiment. The separation between the slits is b and the screen is at a distance d(gtb) from the slits. At a point on the screen directly in front of one of the slits, certain wavelength are missing. Some of these missing wavelength are
Aλ=b2dBλ=2b2dCλ=b23dDλ=2b23dWhite light is used to illuminate the two slits in a Young's double slit experiment. The separation between the slits is b and the screen is at a distance d(>>b) from the slits At a point on the screen directly in front of one of the slits, certain wavelengths are missing some of these missing wavelengths are
Aλ=b2/dBλ=2b2/dCλ=b2/3dDλ=2b2/3dWhite light is used to illuminate the two slits in a Young's
double slit experiment. The separation between the slits is b and the screen is at
a distance d(>>b) from the slits. At a point on the screen directly in front of
one of the slits, certain wavelengths are missing. Some of these missing
wavelength are
(a)λ=b2/d(b)λ=2b2/d(c)λ=b2/3d(d)λ=2b2/3d .Aλ=b2/dBλ=2b2/dCλ=b2/3dDλ=2b2/3d
In a double slit experiment, the distance between the slits is d. The screen is at a distance D from the slits. If a bright fringe is formed opposite to one of the slits, its order is
View SolutionIn Young's double-slit experiment, white light is used. The separation between the slits is d. The screen is at a distance D (D » d) from the slits. Some wavelengths are missing exactly in front of one slit. These wavelengths are
View SolutionIn Young' s double-slit experiment, separation between the two slits is d and separation between plane of the slits and the screen is D. A small hole is made on the screen at a point directly in front of one of the slit. Some wavelengths are missing from the light coming out from hole on the other side. These wavelengths are
View SolutionIn Young's double-slit experiment, the separation between the slits is halved and the distance between the slits and the screen in doubled. The fringe width is
View SolutionIn Young's double slit experiment, the separation between the slits is halved and the distance between the slits and screen is doubled. The fringe-width will :
View Solution
