Light shining through two very narrow slits produces an interference maximum at point P when the entire apparatus is in air as shown in the following figure. For the interference maximum represented, light through the bottom slit travels one wavelength further than light through the top slit before reaching point P. If the entire apparatus is immersed in water, the angle θ to the interference maximum
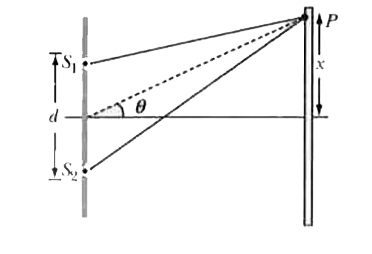
Is unchanged
Decreascs bccausc the frequency decreases
Decreases because the wavelength decreases
Increases because the frequency increases
The correct Answer is:C
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION Book:RESNICK AND HALLIDAYChapter:INTERFERENCE AND DIFFRACTION Exercise:PRACTICE QUESTIONS (More than One Correct Choice Type)
Explore 23 Videos
- INTERFERENCE AND DIFFRACTION Book:RESNICK AND HALLIDAYChapter:INTERFERENCE AND DIFFRACTION Exercise:PRACTICE QUESTIONS (Linked Comprehension)
Explore 21 Videos
- INTERFERENCE AND DIFFRACTION Book:RESNICK AND HALLIDAYChapter:INTERFERENCE AND DIFFRACTION Exercise:PROBLEMS
Explore 61 Videos
- HYDROGEN ATOMBook:RESNICK AND HALLIDAYChapter:HYDROGEN ATOMExercise:PRACTICE QUESTIONS(Integer Type)
Explore 6 Videos
- MAGNETIC FIELDS DUE TO CURRENTSBook:RESNICK AND HALLIDAYChapter:MAGNETIC FIELDS DUE TO CURRENTSExercise:Practice Question (Integer Type)
Explore 4 Videos
Similar Questions
Light of wavelength 520nm passing through a double slit,produced interference pattern of relative intensity versus deflection angle θ as shown in the figure.find the separation of between the slits.
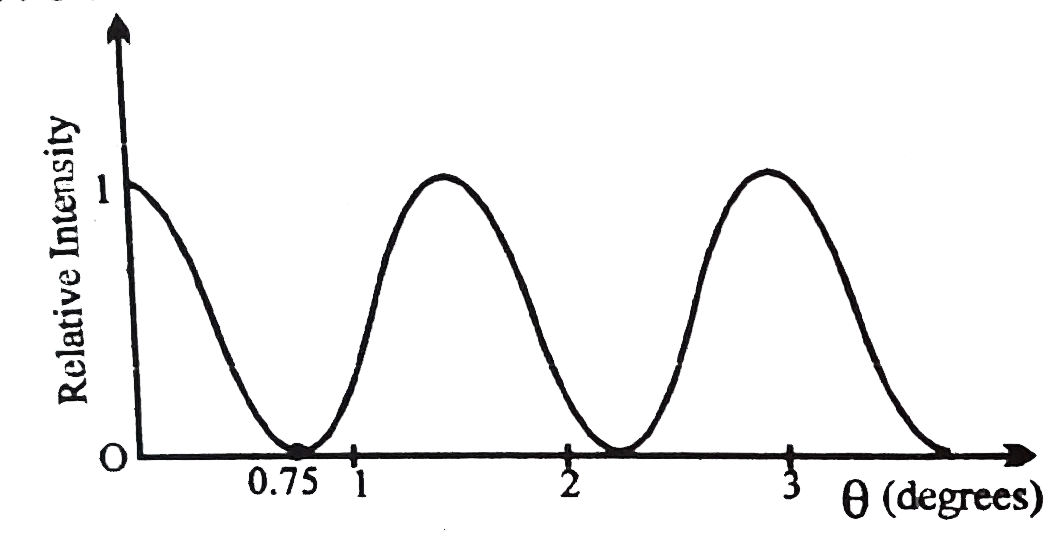
View SolutionLight of wavelength 520nm passing through a double slit,produced interference pattern of relative intensity versus deflection angle θ as shown in the figure.find the separation of between the slits.

View Solution
Knowledge Check
In Young's double-slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is λ and d is the distance between the slits, the angular separation between point P and the center of the screen is
Asin−1(λd)Bsin−1(λ2d)Csin−1(λ3d)Dsin−1(λ4d)
In Young's double slit interference experiment the wavelength of light used is 5000A .If the phase difference between waves reaching a point p on the screen is 6π ,then at the pointp is ?
View SolutionIn double slit experiment, the wavelength λ of the light source 400nm, the slit separation d is 20μm and the individual slit width a is 4μm. Consider the interference of the light from the two slits and also the definition of light through each slit. Find number bright interference fringes are within the central peak of definition envelope.
View SolutionIn a two-slit interference pattern, the maximum intensity is l0.
(a) At a point in the pattern where the phase difference between the waves from the two slits is 60∘, what is the intensity?
(b) What is the path difference for 480nm light from the two slits at a point where the phase angle is 60∘?
View SolutionIn a two-slit interference pattern, the maximum intensity is l0.
(a) At a point in the pattern where the phase difference between the waves from the two slits is 60∘, what is the intensity?
(b) What is the path difference for 480nm light from the two slits at a point where the phase angle is 60∘?
View SolutionIn Young.s double slit interference experiment the wavelength of light used is 6000A0. If the path difference between waves reaching a point P on the screen is 1.5 microns, then at that point P
View SolutionA double slit arrangement produces interference fringes for sodium light (λ=5890Å) that are 0.40∘ apart. What is the angular fringe separation if the entire arrangement is immersed in water?
View SolutionIn Young's double-slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is λ and d is the distance between the slits, the angular separation between point P and the center of the screen is
View Solution
