In Fig. uniform beams A and B are attached to a wall with hinges and loosely bolted together (there is no torque of one on the other). Beam A has length L = 2.40 m and mass 58.0 kg, beam B has mass 70.0 kg. The two hinge points are separated by distance d = 1.80 m. In unit-vec notation, what is the force on (a) beam A due to its hinge, (b) beam A due to the bolt, (c) beam B due to its hinge, and (d) beam B due to the bolt?
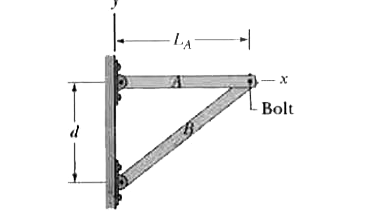
(a) ¯¯¯F=→Fxˆi+→Fyˆj=(−836N)ˆi+(284N)ˆj, (b) →G=→Gxˆi+→Gyˆj=(+836N)ˆi+(284N)ˆj , (c) →H=→Hxˆi+→Hyˆj=(+836N)ˆi+(970N)ˆj , (d) −→G=−→Gxˆi+→Gyˆj=(−836N)ˆi−(284N)ˆj
Topper's Solved these Questions
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS
28 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (More than One Option Correct Type)
2 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - CHECKPOINT
4 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))
3 Videos
- TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)
4 Videos
Similar Questions
A uniform beam of weight W is attached to a verical wall by a hings H. The beam is held hotizontal by a rope as shown below.
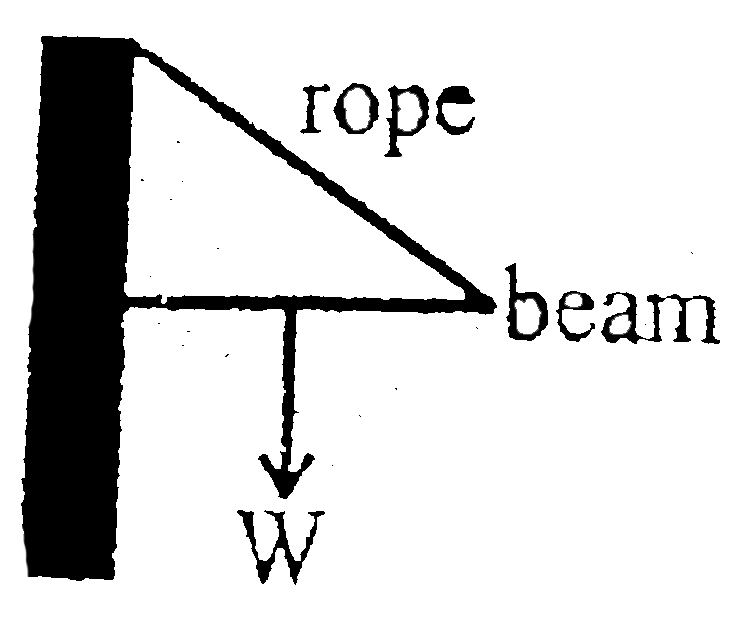
Which one of the following best shows the direction of the reactoin force R at the hings?
View SolutionA uniform wood panel of mass 35.0 kg is hinged ver tically on a wall by two hinges, one 0.300 m from its top and the other 0.300 m from its bottom. The panel is 2.10 m tall and 0.910 m wide. A y axis extends upward through the hinges and an x axis extends outward along the panel's width. If each hinge supports half the panel's weight, what are the forces on the panel at (a) the top hinge and (b) the bottom hinge, both in unit-vec notation?
View Solution
Knowledge Check
A uniform beam of weight W is attached to a verical wall by a hings H. The beam is held hotizontal by a rope as shown below.

Which one of the following best shows the direction of the reactoin force R at the hings?A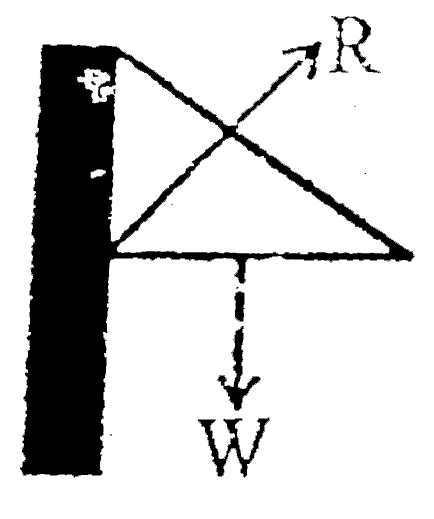 B
B C
C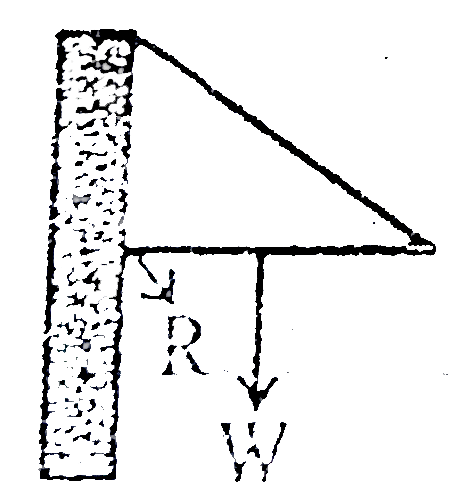 D
D
Two men support a uniform horizontal beam at its two ends, if one of them suddenly lets go, the force exerted by the beam on the other man will
Aremain unaffectedBincreaseCdecreaseDbecome unequal to the force exerted by him on the beamFour uniform spheres, with masses mA=40kg,mB=35kg,mC=200kg , and mD = 50 kg, have (x,y) coordinates of (0, 50 cm), (0, 0), (–80 cm, 0), and (40 cm, 0), respectively. In unit-vector notation, what is the net gravitational force on sphere B due to the other spheres?
A(2.6×10−5N)ˆjB(7.1×10−3N)ˆjC(3.7×10−7N)ˆjD(4.9×10−4N)ˆj
Two men support a uniform horizontal beam at its two ends, if one of them suddenly lets go, the force exerted by the beam on the other man will
View Solutiona uniform beam, of length L and mass m = 1.8 kg, is at rest on two scales. A uniform block, with mass M = 2.7 kg, is at rest on the beam, with its center a distance L/4 from the beam's left end. What do the scales read?
View SolutionBeam expander
Assume that a parallel beam is incident on two convex lens of focal length 20cm and 40cm. The beam has a diameter of 2cm. What should be the distance between them so that the final beam emerges parallel to the principal axis( Fig. 34-46) ?
View SolutionFour uniform spheres, with masses mA=40kg,mB=35kg,mC=200kg , and mD = 50 kg, have (x,y) coordinates of (0, 50 cm), (0, 0), (–80 cm, 0), and (40 cm, 0), respectively. In unit-vector notation, what is the net gravitational force on sphere B due to the other spheres?
View SolutionA beam of hydrogen molecules (H2) is directed toward a wall, at an angle of 32∘ with the normal to the wall. Each molecule in the beam has a speed of 1.0 km/s and a mass of 3.3×10−24 g. The beam strikes the wall over an area of 2.0 cm?, at the rate of 4.0×1023 molecules per second. What is the beam's pressure on the wall?
View Solution
