A uniform cubical crate is 0.850 m on each side and weighs 500 N. It rests on a floor with one edge against a very small, fixed obstruction. At what least height above the floor must a horizontal force of magnitude 400 N be applied to the crate to tip it?
To solve the problem, we need to determine the height at which a horizontal force of 400 N must be applied to the crate to cause it to tip over.
1. Identify the dimensions and weight of the crate:
- The crate is a cube with each side measuring 0.850 m.
- The weight of the crate (W) is 500 N.
2. Determine the center of mass:
- For a uniform cube, the center of mass is located at the geometric center. Since the cube is 0.850 m on each side, the center of mass is at a height of 0.8502=0.425 m from the base.
3. Understand the tipping condition:
- The crate will tip over when the moment caused by the applied force about the pivot point (the edge resting against the obstruction) equals the moment caused by the weight of the crate about the same pivot point.
4. Calculate the moment due to the weight of the crate:
- The moment due to the weight (M_weight) about the pivot point is given by:
Mweight=W×d
where d is the horizontal distance from the pivot point to the center of mass. Since the crate is resting on one edge, d=0.8502=0.425 m.
Mweight=500N×0.425m=212.5N m
5. Calculate the moment due to the applied force:
- The moment due to the applied force (M_force) about the pivot point is given by:
Mforce=F×h
where F=400N is the applied force and h is the height at which the force is applied.
6. Set the moments equal for tipping condition:
- For the crate to tip, the moments must be equal:
Mweight=Mforce
212.5N m=400N×h
7. Solve for h:
h=212.5N m400N=0.53125m
8. Conclusion:
- The least height above the floor at which the horizontal force of 400 N must be applied to tip the crate is approximately 0.531 m.
- The crate is a cube with each side measuring 0.850 m.
- The weight of the crate (W) is 500 N.
- For a uniform cube, the center of mass is located at the geometric center. Since the cube is 0.850 m on each side, the center of mass is at a height of 0.8502=0.425 m from the base.
- The crate will tip over when the moment caused by the applied force about the pivot point (the edge resting against the obstruction) equals the moment caused by the weight of the crate about the same pivot point.
- The moment due to the weight (M_weight) about the pivot point is given by:
Mweight=W×d
where d is the horizontal distance from the pivot point to the center of mass. Since the crate is resting on one edge, d=0.8502=0.425 m.
Mweight=500N×0.425m=212.5N m
- The moment due to the applied force (M_force) about the pivot point is given by:
Mforce=F×h
where F=400N is the applied force and h is the height at which the force is applied.
- For the crate to tip, the moments must be equal:
Mweight=Mforce
212.5N m=400N×h
h=212.5N m400N=0.53125m
- The least height above the floor at which the horizontal force of 400 N must be applied to tip the crate is approximately 0.531 m.
Topper's Solved these Questions
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS
28 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (More than One Option Correct Type)
2 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - CHECKPOINT
4 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))
3 Videos
- TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)
4 Videos
Similar Questions
A train starting from rest is moving along a straight track with a constant acceleration fo 2.5m/s2. A passenger at rest in the train observes a particle of mass 2kg to be at rest on the floor with which it has a coefficient of friction μs=μk=0.5 .Six seconds after the starting of the train , a horizontal force F = 13N is applied to the particle for two seconds duration. The passenger now observes the particle to move perpendicular to the direction of the train.
(a) calculate the kinetic energy of the particle with respect to the passenger at the end of 8 seconds after starting of the train.
( b) repeat the calculate of ( a) for an observer on the ground.
View SolutionA cubical block of side a and of mass m rests on a rough horizontal surface. A horizontal force F is applied to normal to one of the faces at height h above the base h>a/2. What is the minimum value of F for which the cube begins to tip about an edge?
View Solution
Knowledge Check
A block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
A8.8NB5.8NC2.8ND10.8NA uniform cube of side 'b' and mass M rest on a rough horizontal table. A horizontal force F is applied normal to one of the face at a point, at a height 3b/4 above the base. What should be the coefficient of friction (μ) between cube and table so that is will tip about an edge before it starts slipping ?
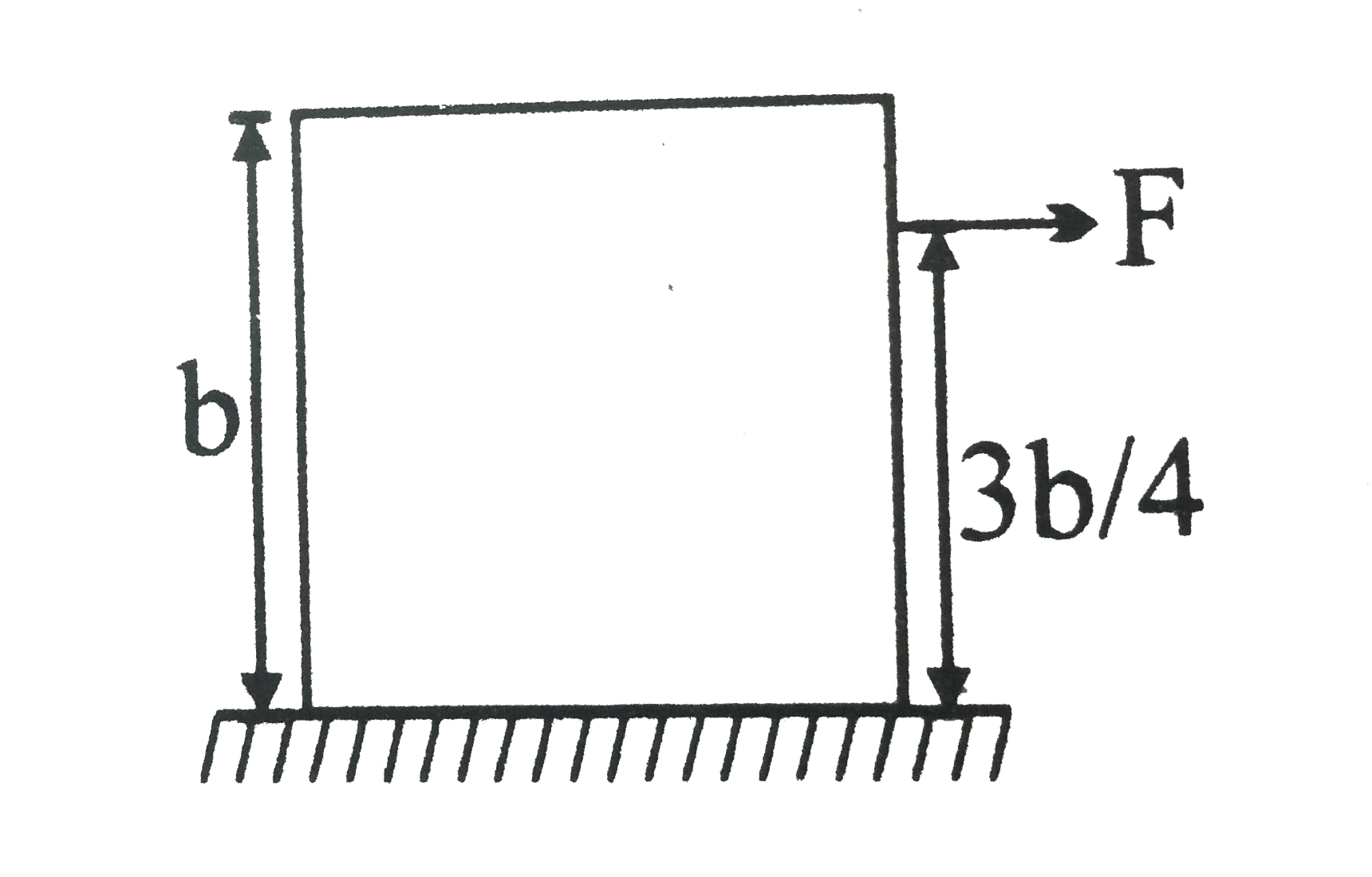 .Aμ>23Bμ>13Cμ>32Dnone
.Aμ>23Bμ>13Cμ>32DnoneA uniform cube of side a and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point directly above the centre of the face, at a height 3a4 above the base. What is the minimum value of F for which the cube begins to tip about an edge?
AmgBmg3C2mg3D5mg3
A box of bananas weighing 40.0Nrests on a horizontal surface is 0.40 and the coefficient of kinetic friction is 0.20
a. If no horizontal force is applied to the box and the box is at rest , how large is the friction force excered on the box ?
b. What is the magnitude of the friction forces if a monkey applies a horizontal force of 6.0N to the box and the box is initial at rest?
c. What minimum horizontal force must the monkey apply to start the box in motion ?
d. What minimum horizontal force must the monkey apply to keep the box moving at constant velocity once it has been starts?
e. If the monkey applies a horizontal force of 18.0N What is the magnitude of the friction force and what is the box's acceleration ?
View SolutionA small cubical block is placed on a triangular block M so that ,they touch each other along a smooth inclined contact plane as shown. The, inclined surface makes an angle θ With the horizontal. A hqrizontal force F is to be applied on the block mi so that the two bodies move without slipping against each other. Assuming the floor to be smooth also, determine the

(a) normal force with which m and M press against each other and
(b) the magnitude of external force F. Express your answer in terms of m, M, θ and g.
View SolutionA uniform cube of side a and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point that is directly above the centre of the face, at a height 3a/4 above the base. The minimum value of F which the cube begins to tip about the edge is ....(Assume that the cube does not slide).
View SolutionAn overweight acrobat, weighing in at 115 kg, wants to perform a single hand stand. He tries to cheat by resting one foot against a smooth frictionless vertical wall. The horizontal force there is 130 N. What is the magnitude of the force exerted by the floor on his hand? Answer in N.
View SolutionA uniform cube of side and mass m rests on a rough horizontal surface. A horizontal force F is applied normal to one face at point that is directly above the centre of the face at a height a4 above the centre. The minimum value of F for which the cube begins to topple above an edge without sliding is
View Solution
