In a ball is thrown leftward from the left edge of the roof, at height h above the ground. The ball hits the ground 1.50 s later, at distance d = 25.0 m from the building and at angle with the horizontal. (a) Find h. (Hint: One way is to reverse the motion, as if on video.) What are the (b) magnitude and ( c) angle relative to the horizontal of the velocity at which the ball is thrown? (d) Is the angle above or below the horizontal?

(a) 32.3 m, (b) 21.9 m/s, ( c) , (d) below
Topper's Solved these Questions
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
49 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
3 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - CHECKPOINT
3 Videos
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )
3 Videos
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions
57 Videos
Similar Questions
A ball is thrown upwards with a speed u from a height h above the ground.The time taken by the ball to hit the ground is
View SolutionA ball is thrown up onto a roof, landing 4.50 s later at height h = 20.0 m above the release level. The ball's path just before landing is angled at θ=60.0∘ with the roof. (a) Find the horizontal distance d it travels. What are the (b) magnitude and ( c) angle (relative to the horizontal) of the ball's initial velocity?
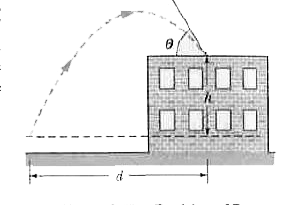
View Solution
Knowledge Check
A ball is thrown upwards with a speed u from a height h above the ground.The time taken by the ball to hit the ground is
A√2h/gB√8h/gC√u2+2ghgDug+√2hgA ball is thrown upwards at an angle of 60∘ to the horizontal. It falls on the ground at a distance of 90 m . If the ball is thrown with the same initial velocity at an angle 30∘, it will fall on the ground at a distance of
A30mB60mC90mD120mA ball released from rest from the roof of a building of height 45 m at t = 0. Find the height of ball from ground at t = 2s.
A10 mB20 mC25 mD30 m
A baseball is hit at a height h = 1.00 m and then caught at the same height. It travels alongside a wall, moving up past the top of the wall 1.00 s after it is hit and then down past the top of the wall. 4.00 s later, at distance D = 50.0 m farther along the wall. (a) What horizontal distance is traveled by the ball from hit to catch? What are the (b) magnitude and ( c) angle (relative to the horizontal) of the ball's velocity just after being hit? (d) How high is the wall?

View SolutionA ball is shot from the ground into the air. At the height of 9.1 m, its velocity is v=(7.6m/s)ˆi+(6.1m/s)ˆj, withˆi horizontal and j upward. (a) To what maximum height does the ball rise? (b) What total horizontal distance does the ball travel? What are the (c) magnitude and (d) angle (below the horizontal) of the ball's velocity just before it hits the ground?
View SolutionA ball is projected from the floor of a long hall having a roof height of H=10m. The ball is projected with a velocity of u=25ms–1 making an angle of θ=37∘ to the horizontal. On hitting the roof the ball loses its entire vertical component of velocity but there is no change in the horizontal component of its velocity. The ball was projected from point A and its hits the floor at B. Find distance AB.
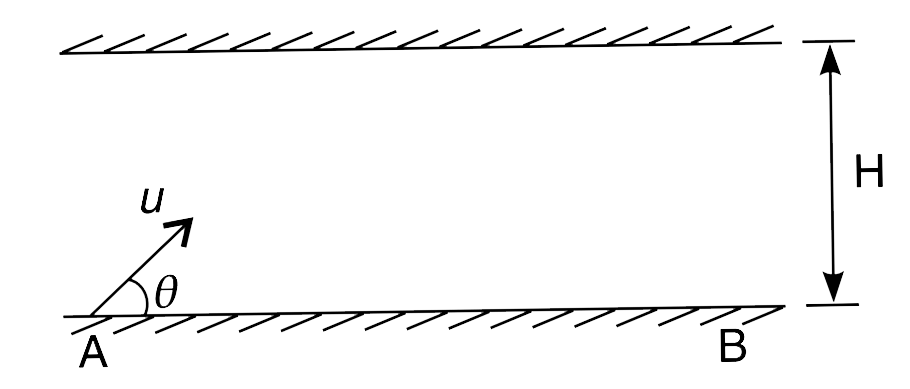
View SolutionYou throw a ball toward a wall at speed 25.0 m/s and at angle θ0=40.0∘ above the horizontal. The wall is distance d = 22.0 m from the release point of the ball. (a) How far above the release point does the ball hit the wall? What are the (b) horizontal and ( c) vertical components of its velocity as it hits the wall? (d) When it hits, has it passed the highest point on its trajectory?

View SolutionA ball is thrown from the ground with a velocity of 20√3 m/s making an angle of 60∘ with the horizontal. The ball will be at a height of 40 m from the ground after a time t equal to (g=10ms−2)
View Solution
