If W1:W2=2:3 and W1:W3=1:2 then W2:W3 is
3:4
4:3
2:3
4:5
The correct Answer is:A
To solve the problem, we need to find the ratio W2:W3 given the ratios W1:W2=2:3 and W1:W3=1:2.
1. Express the Ratios in Terms of a Common Variable:
- From the ratio W1:W2=2:3, we can express:
W1=2xandW2=3x
- Here, x is a common variable.
2. Express W3 in Terms of W1:
- From the ratio W1:W3=1:2, we can express:
W1=1yandW3=2y
- Here, y is another common variable.
3. Equate the Expressions for W1:
- Since both expressions represent W1, we can set them equal to each other:
2x=1y⇒y=2x
4. Substitute y back to find W3:
- Now substitute y in the expression for W3:
W3=2y=2(2x)=4x
5. Now we have all weights in terms of x:
- W1=2x
- W2=3x
- W3=4x
6. Find the Ratio W2:W3:
- Now we can find the ratio:
W2:W3=3x:4x=3:4
Final Answer:
Thus, the ratio W2:W3 is 3:4.
- From the ratio W1:W2=2:3, we can express:
W1=2xandW2=3x
- Here, x is a common variable.
- From the ratio W1:W3=1:2, we can express:
W1=1yandW3=2y
- Here, y is another common variable.
- Since both expressions represent W1, we can set them equal to each other:
2x=1y⇒y=2x
- Now substitute y in the expression for W3:
W3=2y=2(2x)=4x
- W1=2x
- W2=3x
- W3=4x
- Now we can find the ratio:
W2:W3=3x:4x=3:4
Thus, the ratio W2:W3 is 3:4.
Similar Questions
If W1:W2=2:3 and W1:W3=1:2 the W2:W3 is 3:4 b. 4:3 c. 2:3 d. 4:5
View SolutionWhich of the following can be the valid assignment of probability for outcomes of sample space, S={W1,W2,W3},{ where W1,W2 and W3 are mutually exclusive events
Assignment
w1w2w3(a)0.40.20.8(b)001(c)−123412(d)121214
View Solution
Knowledge Check
W1,W2 and W3 are the different sizes of windows 1,2, and 3 respectively placed in a vertical plane. A particle is thrown up in the vertical plane. Let t1,t2 and t3 are the time taken to cross the window W1,W2 and W3 respectively and ΔV1,ΔV2 and ΔV3 are the change in speed after respective window cross.
 AAverage speed of the particle passing the windows may be equal if W1<W2<W3BAverage speed of the particle passing the windows may be equal if W1>W2>W3CIf W1=W2=WP3, the change in speed of the particle while crossing the windows will satisfy ΔV1<ΔV2<ΔV3DIf W1=W2=W3, the time taken by particle to cross the windows will satisfy t1<t2<t3
AAverage speed of the particle passing the windows may be equal if W1<W2<W3BAverage speed of the particle passing the windows may be equal if W1>W2>W3CIf W1=W2=WP3, the change in speed of the particle while crossing the windows will satisfy ΔV1<ΔV2<ΔV3DIf W1=W2=W3, the time taken by particle to cross the windows will satisfy t1<t2<t3The value of (1+ω2+2ω)3n−(1+ω+2ω)3n is equal to
A0B1CωDω2If W1W2,W3andW4 are work done in isothermal, adiabatic, isobaric and isochoric reversible process, the correct order (for expansion) will be
AW1>W2>W3>W4BW3>W2>W1>W4CW3>W2>W4>W1DW3>W1>W2>W4
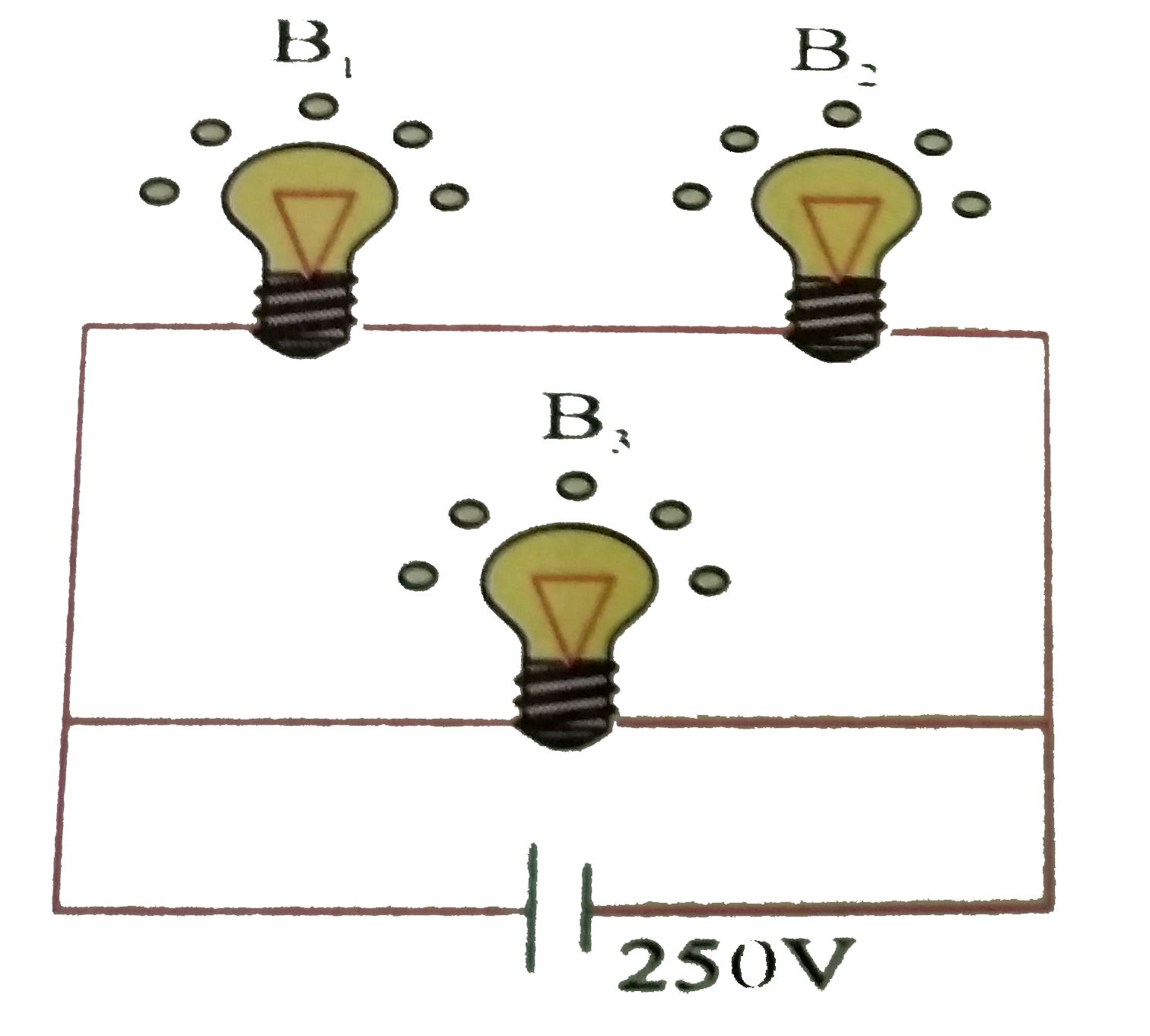
A 100 W bulb B1 and two 60 W bulbs B2 and B3, are connected to a 250V source, as shown in the figure now W1,W2 and W3 are the output powers of the bulbs B1,B2 and B3 respectively then
View Solution(2+ω+ω2)3+(1+ω−ω2)3=(1−3ω+ω2)4=1
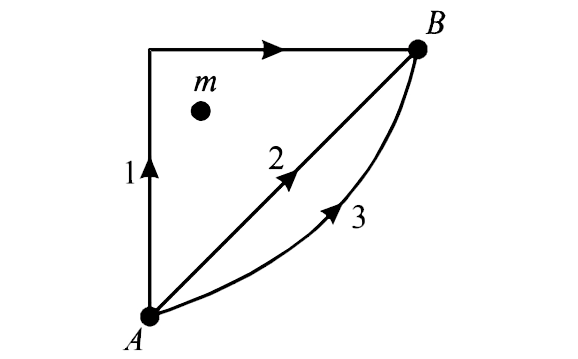
View SolutionIf W1W2 and W3 represent the work done in moving a particle from A to B along three different paths 1.2 and3 respectively (as shown ) in the gravitational fieled of a point mass m, find the correct relation between W_(1) W_(2)andW_(3)
View SolutionIf ω is a non-real cube root of unity, then Δ=∣∣ ∣ ∣∣a1+b1ωa1ω2+b1a1+b1+c1ω2a2+b2ωa2ω2+b2a2+b2ω+c2ω2a3+b3ωa3ω2+b3a3+b3ω+c3ω2∣∣ ∣ ∣∣ is equal to
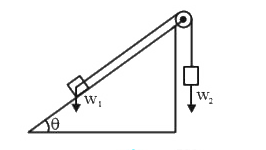
View SolutionIn the accompanying diagram W1 is 5kg weight and W2 is 3 kg weight. If the component of W1 parallel to the incline is equal to W2, then the angle θ is nearly :
View Solution
