Question

For points $P=(x_1,y_1)\text{and}Q=(x_2,y_2)$ of the coordinate plane, a new distance $d(P,Q)$ is defined by $d(P,Q)=|x_1-x_2|+|y_1-y_2|.$ Let $O(0,0)$ and $A=(3,2)$. Prove that the set of points in the first quadrant which are equidistant (wrt new distance) from $O$ and $A$ consists of the union of a line segment of finite length and an infinite ray. Sketch this set in a labelled diagram.

Explanation

Note `d : (P,Q)=|x_(1)-x_(2)|+|y_(1)-y_(2)|`
It is new method of representing distance between two points `P` and `Q` and in future very important in coordinate geometry.
Now, let `P(x,y)` be any point in the first quadrant. We have
`d(P,0)=|x-0|+|y-0|=|x|+|y|=x+y` `[ :'x,y gt 0]`
`d(P,A)=|X-3|+|Y-2|` [given]
`d(P,0)=d(P,A)` [given]
`impliesx+y=|x-3|+|y-2|`......`(i)`
Case I When `o lt x lt 3`, `o lt y lt 2`
In this case, Eq. `(i)` becomes
`x+y=3-x+2-y`
`implies 2x+2y=5`
or `x+y=5//2`
Case II When `0 lt x lt 3`, `y ge 2`
Now, Eq. `(i)` becomes
`x+y=3-x+y-2`
`implies2x=1`
`implies x=1//2`
Case III When `x ge 3`, `0 lt y lt 2`

Now, Eq. `(i)` becomes
`x+y=x-3+2-y`
`implies2y=-1` or `=-1//2`
Hence, no solution .
Case IV When `x ge 3`, `y ge 2`
In this case, case I changes to
`x+y=x-3+y-2implies0=-5`
which is not possible.
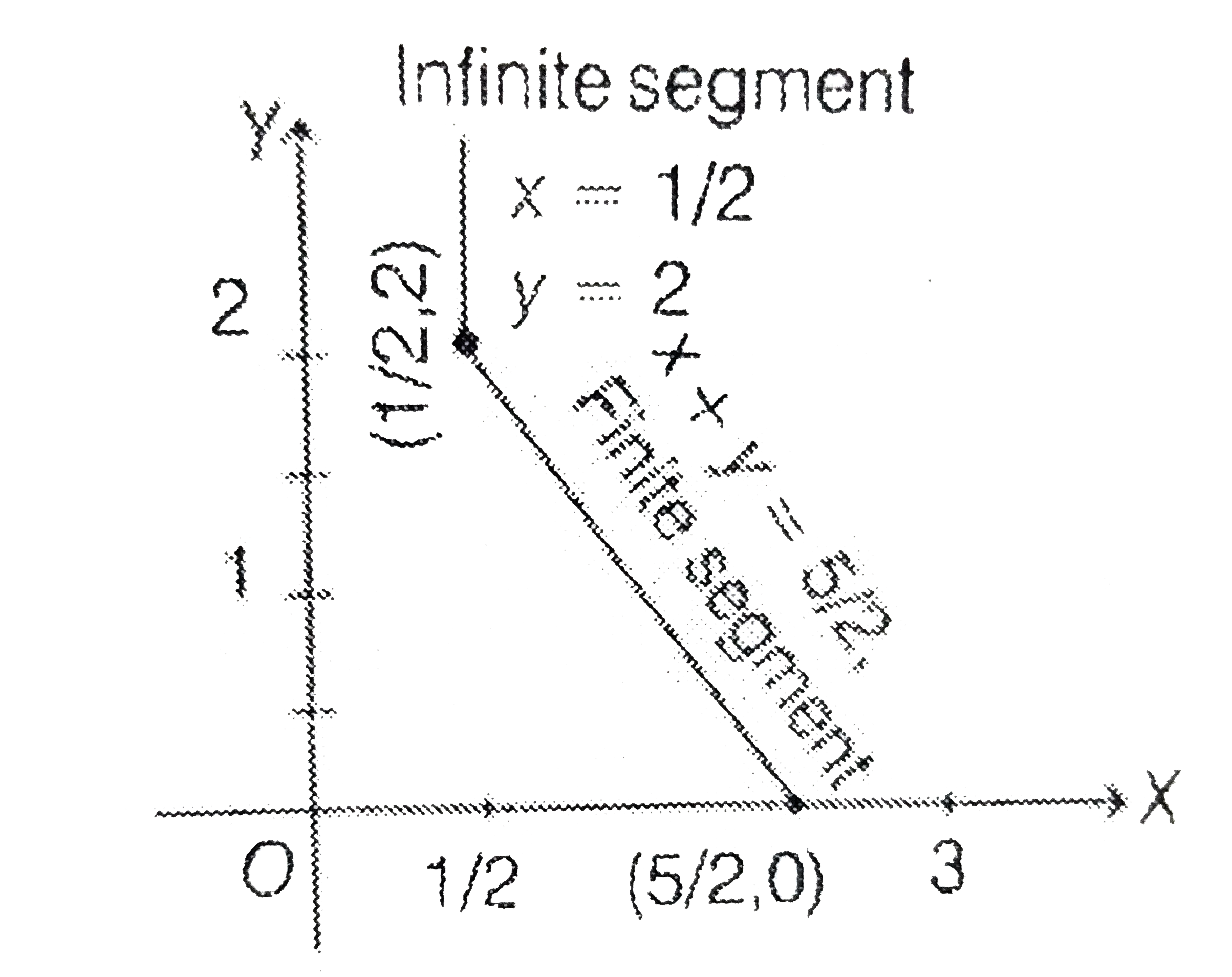
Hence, the solution set is
`{(x,y)|x=12`, `y ge 2 }uu}(x,y)}|`
`x+y=5//2`, `0 lt x lt 3`, `0 lt y gt 2`
The graph is given in adjoining figure.