One of the diameter of a circle circumscribing the rectangle ABCD is $4 y = x + 7$ , If A and B are the points $(- 3, 4)$ and $(5, 4)$ respectively, then the area of rectangle is

Video Solution

Text Solution

Verified by Experts

Let $O$ be the centre and $M$ be mid-point of $A B$ .

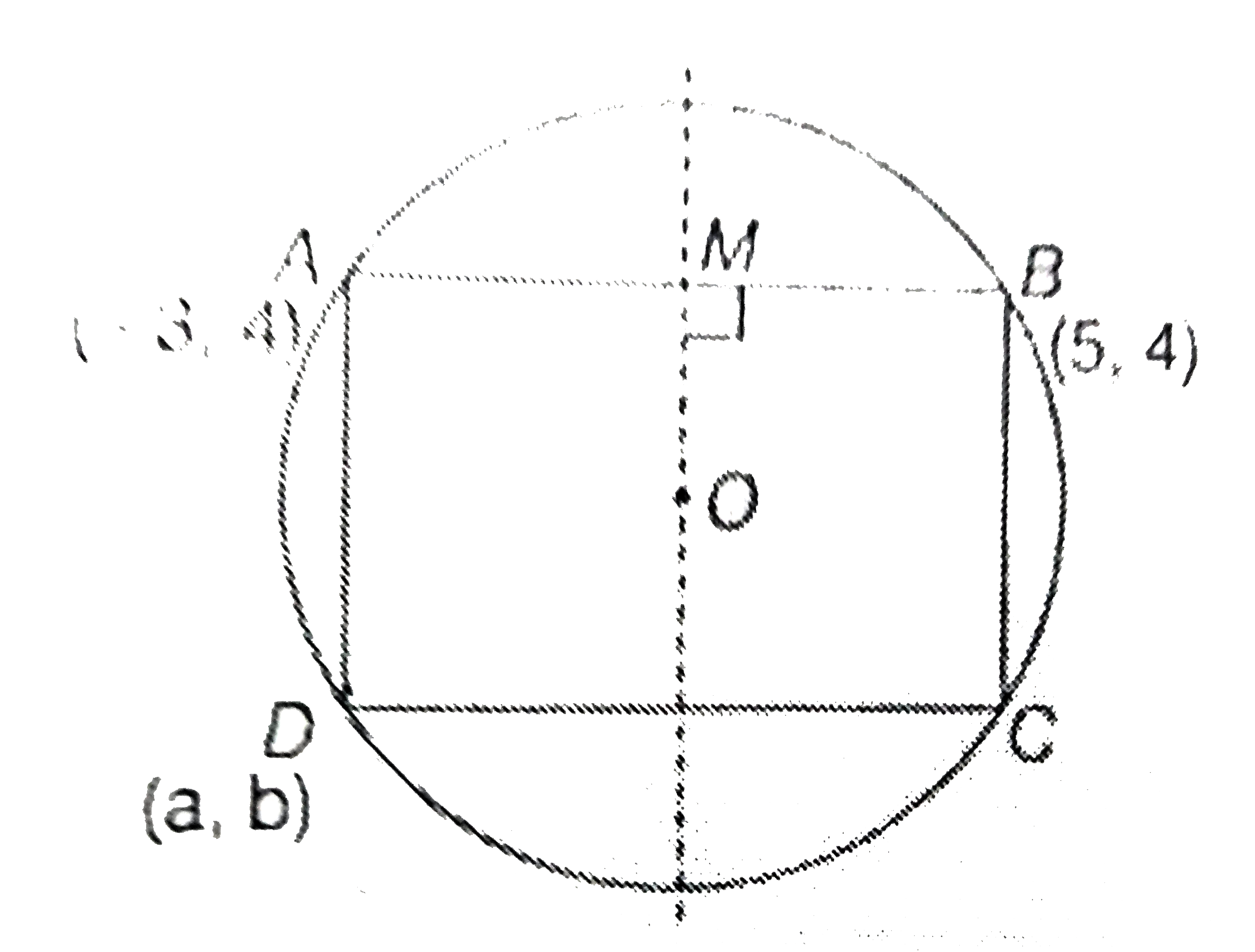
Then, $O M ⊥ A B \Rightarrow M (1, 4)$
Since, slope of $A B = 0$
Equation of straight line $M O$ is $x = 1$ and equation of diameter is $4 y = x + 7$ .
$\Rightarrow$ Centre is $(1, 2)$ . Also, $O$ is mid-point of $B D$
$\Rightarrow (\frac{α + 5}{2}, \frac{β + 4}{2}) = (1, 2) \Rightarrow α = - 3$ , $β = 0$
$∴ A D = \sqrt{{(- 3 + 3)}^{2} + {(4 - 0)}^{2}} = 4$
and $A B = \sqrt{64 + 0} = 8$
Thus, area of rectangle $= 8 \times 4 = 32$ sq units

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINE AND PAIR OF STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The sum of length and breadth of a rectangle is 16 cm. A circle is circumscribed on the rectangle. If the ratio of area of the circumcircle to that of the rectangle is $73 : 35$ , the area of the rectangle is (in $c m^{2}$ )
A128
B174
C55
D256

IIT JEE PREVIOUS YEAR-STRAIGHT LINE AND PAIR OF STRAIGHT LINES-VARIOUS FORMS OF STRAIGHT LINE (Analytical & Desriptive Questions)

Home
Ask Doubt
Profile