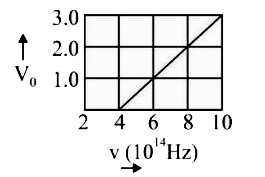
The stopping potential V0 (in volt ) as a function of frequeny (v) for a sodium emitter, is shown in the figure.
The work functio (in eV) of sodium, from the data plotted in the figure will be
(Given Plank's constant (h)=6.63×10−34 Js, electron charge e=1.6×10−19C)

f0=4×1014Hz ,
W0=hf0=6.63×10−34×(4×1014)J
=(6.63×10−34)×(4×1014)1.6×10−19
=1.66eV
Topper's Solved these Questions
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 26 : (ATOMS)
15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 27 : (NUCLEI)
15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 24 : (WAVE OPTICS)
15 Videos
- ATOMSBOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR
30 Videos
- COMMUNICATION SYSTEM BOOK - DISHA PUBLICATIONCHAPTER - COMMUNICATION SYSTEM EXERCISE - EXERCISE-2 : Concept Applicator
30 Videos
Similar Questions
The stopping potential V0 (in volt) as a function of frequency (v) for a sodium emitter, is shown in the figure. The work function of sodium, from the data plotted in the figure, will be:
(Given : Planck’s constant)
(h)=6.63×10−34Js electron charge e=1.6×10−19C)
View SolutionThe stopping potential V0 (in volt) as a function of frequency (v) for a sodium emitter, is shown in the figure. The work function of sodium, from the data plotted in the figure, will be:
(Given : Planck’s constant)
(h)=6.63×10−34Js electron charge e=1.6×10−19C)

View Solution
Knowledge Check
The work function of a photoelectric material is 3.3 V. the threshold frequency will be equal to [Given that h=6.6×10−34Js]
A8.0×1014HzB8.0×1034HzC5.0×1015HzD5.0×1019HzThe momentum of a photon of de Broglie wavelength 5000Å is …………… .
[Plank's constant =6.63×10−34J.s]A1.326×10−28kg−m/sB7.54×10−28kg−m/sC1.326×10−27kg−m/sD7.54×10−27kg−m/sThe electric field of certain radiation is given by the equation E=200{sin(4π×1010)t+sin(4π×1015)t}
falls in a metal surface having work function 2.0 eV. The maximum kinetic energy 2.0 eV. The maximum kinetic energy (in eV) of the photoelectrons is [Plank's constant (h)=6.63×10−34Js and electron charge e=1.6×10−19C]A3.3B4.3C5.3D6.3
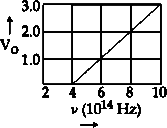
the stopping potential Vo (in volt) as a function of frequency (v) for a soidum emitter, is shown in the figure. The work function of sodium from the data plotted in the figure. Will be:
[ given plank's constant (h)=6.63×10−34Js, electron charge e=1.6×10−19C)
View SolutionCalculate the speed of the electron in the first Bohr orbit given that h=6.6×10−34Js,m=9.11×10−31kg and e=1.603×10−19C.
View SolutionThe electric field of certain radiation is given by the equation E=200{sin(4π×1010)t+sin(4π×1015)t}
falls in a metal surface having work function 2.0 eV. The maximum kinetic energy (in eV) of the photoelectrons is [Plank's constant (h)=6.63×10−34Js and electron charge e=1.6×10−19C]
View Solutionin the question number 63, the frequency of emitted photon due to the given transition is (h=6.64×10−34Js,1eV=1.6×10−19J)
View Solutionin the question number 63, the frequency of emitted photon due to the given transition is (h=6.64×10−34Js,1eV=1.6×10−19J)
View Solution
