In a right triangle ABC, right angled at B,the ratio of AB:ACis 1:√2. Find the value of2tanA1+tan2A
14
12
4
1
The correct Answer is:D
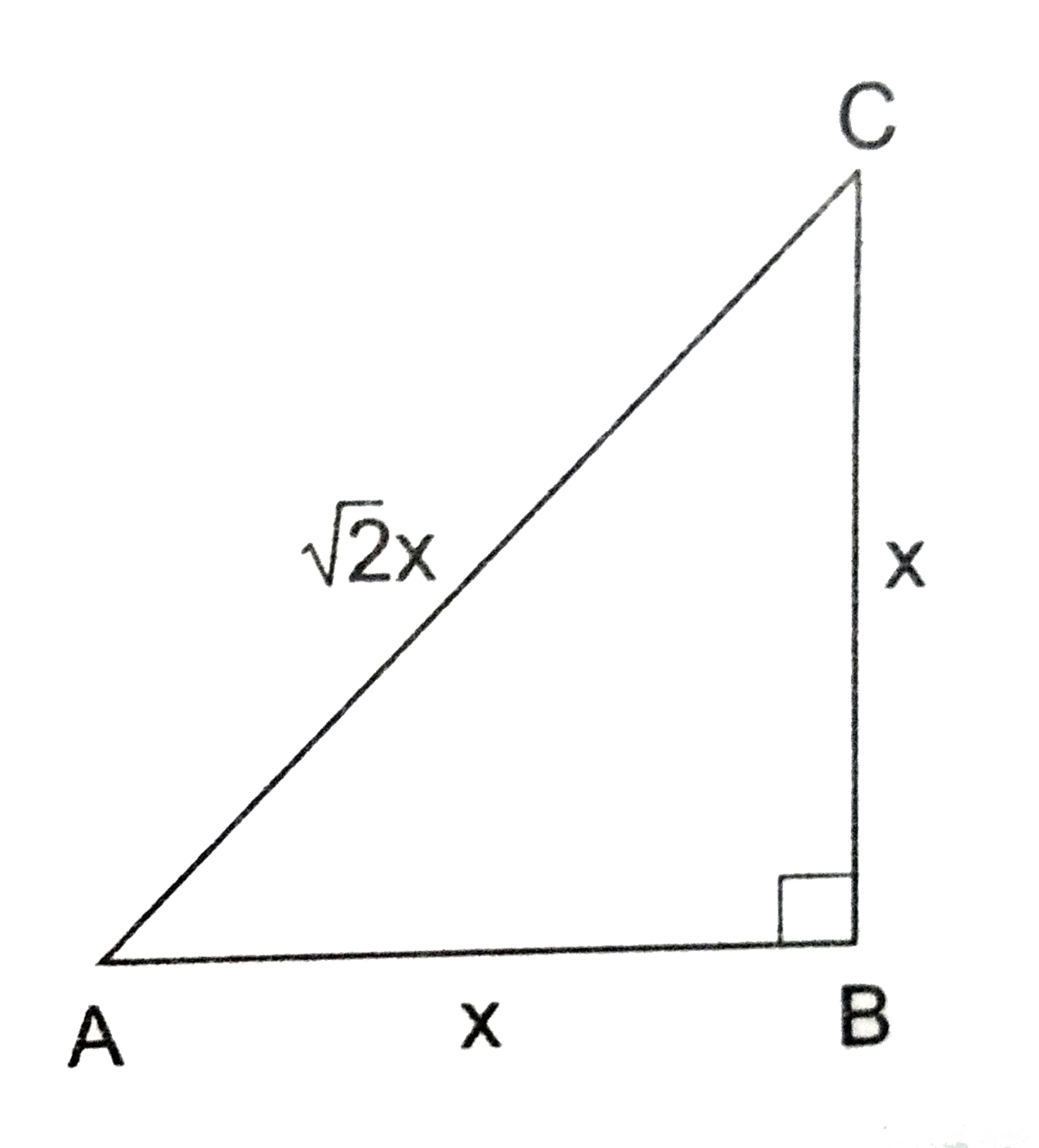
Consider aΔABCin which ∠B=90∘andAB:AC=1:√2.
Let AB=x,Then,AC=√2x.
By pythagoras' theorem , we have
AC2=AB2+BC2⇒BC2=AC2−AB2
⇒BC2=(√2x)2−(x)22x2−x2=x2
⇒BC=x.
∴tanA=BCAB=xx=1.
SO , the given expression =(2tanA1+tan2A)=(2×11+1)=22=1.
Topper's Solved these Questions
- TRIGONOMETRIC RATIOSBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOSEXERCISE - Exercise 10
35 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
- TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES EXERCISE - Exercise 12
15 Videos
Similar Questions
Knowledge Check
Let triangle ABC be right angled at C.If tanA+tanB2, then-
A∠A=30∘Btriangle ABC must be isosclesCsides of the triangle ABC are 3,4,5Dtriangle must be scalene
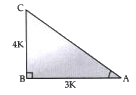
△ABC is a right triangle , right angle at B . Given the ratio of altitude and base tanA=43 . Find the value of (1+tan2A)
View SolutionIn a right triangle ABC, right-angled at B, if sin(A−C)=12 find the measures of angles A and C
View SolutionIn a right triangle ABC right angled at B , ∠ACB=θ , AB=2cm and BC=1 cm . Find the value of sin2θ+tan2θ .
View SolutionIn a right-angled triangle ABC, right angled at B, AB = x2, BC = x+2 and AC = x+3. Find value of x.
View Solution
ΔABC is a right triangle , right angle at B . Given the ratio of altitude and base tanA=43 . Find the value of AC
View SolutionIn triangle ABC, right-angled at B. if tanA=1√3,find the value of:sinAcosC+cosAsinC
View SolutionIn a right triangle ABC , right angled at C , if ∠B=60o and AB=15 units. Find the remaining angles and sides.
View Solution
