Question

In a triangle ${\displaystyle ABC,DandE}$
are points on ${\displaystyle BCandAC,}$
respectivley, such that ${\displaystyle BD=2DCandAE=3EC\stackrel{.}{}}$
Let ${\displaystyle P}$
be the point of intersection of ${\displaystyle ADandBE\stackrel{.}{}}$
Find ${\displaystyle BP/PE}$
using the vector
method.

Answer

`(8)/(3)`

Explanation

Let the position vectors of A,B and C are `vec(a) , vec(b) " and " vec( c) `
respectively since the point D divides BC in the ratio of 2: 1 the position vector of D will be

`E = ((2vec( c) + vec(b))/(3))`
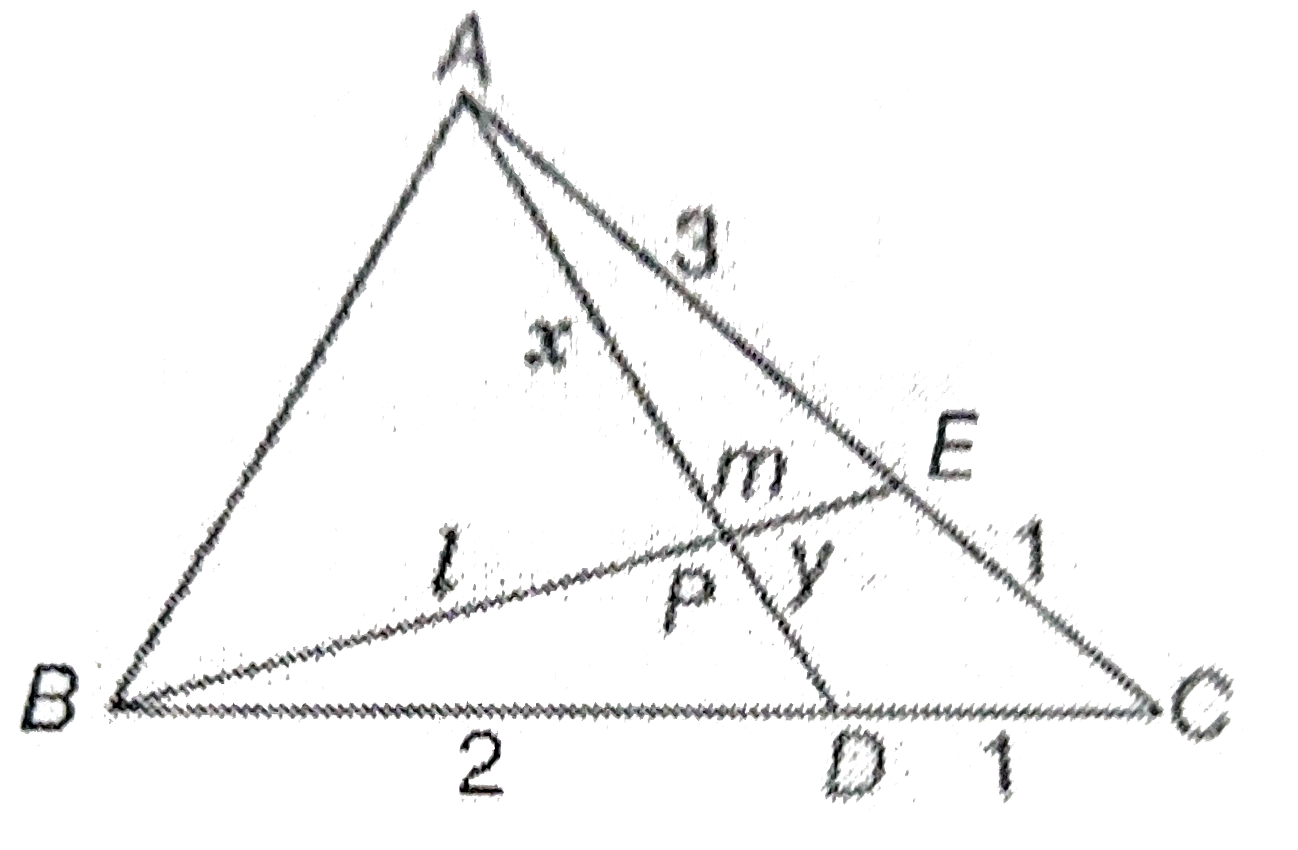
and the point E divides AC in the ratio 3: 1
therefore `E= ((3 vec( c) + vec( a))/(4))`
Now let P divides BE is the ratio l : m and AD in the ratio x: y
Hence the position vector of P getting from BE and AD must be the same .
Hence we have
`(l(((3vec(c ) + vec(a)))/(4))+m vec(b))/(l+ m) = (x ((2 vec(c ) + vec(b))/(3))+ y vec(a))/(x+y)`
`rArr ((3lvec(v))/(4)+ (lvec(a))/(4)+ vec(b))/(l+m) = ((2 vec(c ) x)/(3)+ (vec(b) x)/(3) + y vec(a))/(x+y)`
`rArr (3l)/(4(l+m))vec(c )+ (l)/(4(l+m)) vec(a) + (mvec(b))/(l+m)`
`=(2x)/(3(x+y)) vec(c ) + (x)/(3(x+y)) vec(b) + (y)/((x+y)) vec(a)`
Now comparing the coefficients we get
`(3l)/(4(l+m)) = (2x)/(3(x+y)) " ".....(i)`
` (l)/(4(l+m)) + (y)/(x+y) " ".....(ii)`
`" and " (m)/(l+m) = (x )/( 3(x+ y)) " ".....(iii)`
On dividing Eq . (i) by Eq . (iii) , we get
`((3l)/(4(+m)))/((m)/(l+m))= ((2x)/(3(x+y)))/((x)/(3(x+y)))`
`rArr (3)/(4). (l)/(m) =2 rArr (l)/(m) =(8)/(3)= (BP)/(PE)`