In a △OAB,E is the mid point of OB and D is the point on AB such that AD:DB=2:1 If OD and AE intersect at P then determine the ratio of OP:PD using vector methods
The correct Answer is:(3:2)
Let O be origin and →A=→a,−−→OB=→b
−−→OE=→b2 [Since E being mid- point of −−→OB]
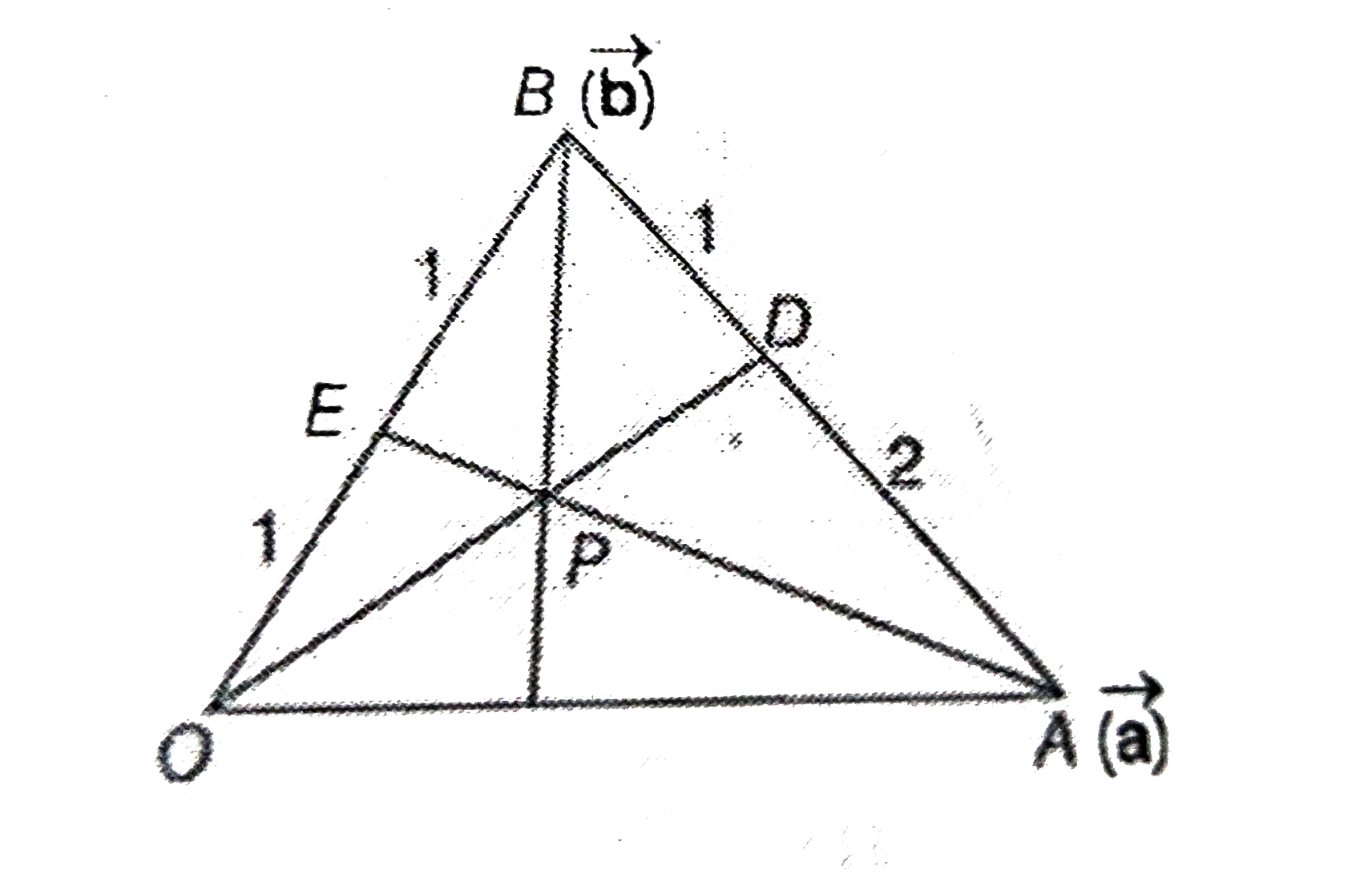
−−→OD=→a.1+→b.21+2
(since D divides −−→AB in the ratio of 2:1)
⇒ Equation of −−→OD is →r=t(→a+2→b3)
and equation of −−→AE is →r=→a+s(→b2−a)
if −−→OD and −−→AE intersect at P then there must be some →r for which they are equal .
⇒t(→a+2→b3)=→a+s(→b2−→a)
⇒t3=1−sand 2t3=s2
⇒t=35 and s=45
∴ Point P is →a+2→b5
Since P divides −−→OD in the ratio of λ:1
∴λ(→a+2→b3)+1.0λ+1=(→a+2→b5)
from Eqs. (i) and (ii)
λ3(λ+1)=15
⇒5λ=3λ+3
⇒λ=32
∴OPPD=32
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - IIT JEE PREVIOUS YEARCHAPTER - VECTOR ALGEBRAEXERCISE - Scalar Product of two vectors (Interger Answer Type Questions )
2 Videos
- VECTOR ALGEBRABOOK - IIT JEE PREVIOUS YEARCHAPTER - VECTOR ALGEBRAEXERCISE - Vector Product of Two Vectors (Objective Questions I)
12 Videos
- VECTOR ALGEBRABOOK - IIT JEE PREVIOUS YEARCHAPTER - VECTOR ALGEBRAEXERCISE - Scalar Product of two vectors (Fill in the Blanks)
3 Videos
- TRIGONOMETRICAL RATIOS AND IDENTITIESBOOK - IIT JEE PREVIOUS YEARCHAPTER - TRIGONOMETRICAL RATIOS AND IDENTITIESEXERCISE - HEIGHT AND DISTANCE
10 Videos
Similar Questions
In a △OAB, E is the mid-point of BO and D is a point on AB such that AD : DB = 2:1. If OD and AE intersect at P, determine the ratio OP: PD using vector method.
View SolutionIn a triangle ABC,DandE are points on BCandAC, respectivley, such that BD=2DCandAE=3EC. Let P be the point of intersection of ADandBE. Find BP/PE using the vector method.
View Solution
Knowledge Check
In a triangle OAB, E is the midpoint of OB and D is a point on AB such that AD:DB=2:1. IF OD and AE intersects at P, then ratio of OPPD is equal to
A3:2B2:3C3:4D4:3In a ΔABC,D is the mid - point of BC and E is mid - point of AD, BF passes through E. What is the ratio of AF:FC?
 A1:1B1:2C1:3D2:3
A1:1B1:2C1:3D2:3D,E,F are the mid points of BC,CAandAB of ΔABC. If ADandBE intersect in G, then AG+BG+CG is equal to
AAD=BE=CFB23(AD+BE+CF)C32(AD+BE+CF)D13(AD+BE+CF)
In ΔABC,D is point on side AB and E is a point on side AC such that ∠ADE=∠ABC,AD=2,BD=3 and AE=3, then what is the value of CE ?
View SolutionIn the given figure ∠ABC=∠BAC , D and E are pointts on BC and AC respectively such that DB = AE . If AD and BE intersect at O then prove that OA = OB
View SolutionGiven that AD is the median on BC of ΔABC,point on AD such that AE=13AD. The line CE intersects AB at F. If AF=1.2cm, find the length of AB.
View SolutionABCD is a parallelogram. E is a point on BC such that BE : EC = m:n. If AE and DB intersect in F, then what is the ratio of the area of triangle FEB to the area of triangle AFD?
View SolutionIf D is a point on the side AB of ABC such that AD:DB=3:2 and E is a point on BC such that DEAC . Find the ratio of areas of ABC and BDE .
View Solution
