Let OACB be a parallelogram with O at the origin andOC a diagonal. Let D be the midpoint of OA. using vector methods prove that BDandCO intersect in the same ratio. Determine this ratio.
The correct Answer is:(2:1)
OA CB is a parallelogram with O is origin . Let
−−→OA=→a,−−→OB=→b,−−→OC=→a+→b
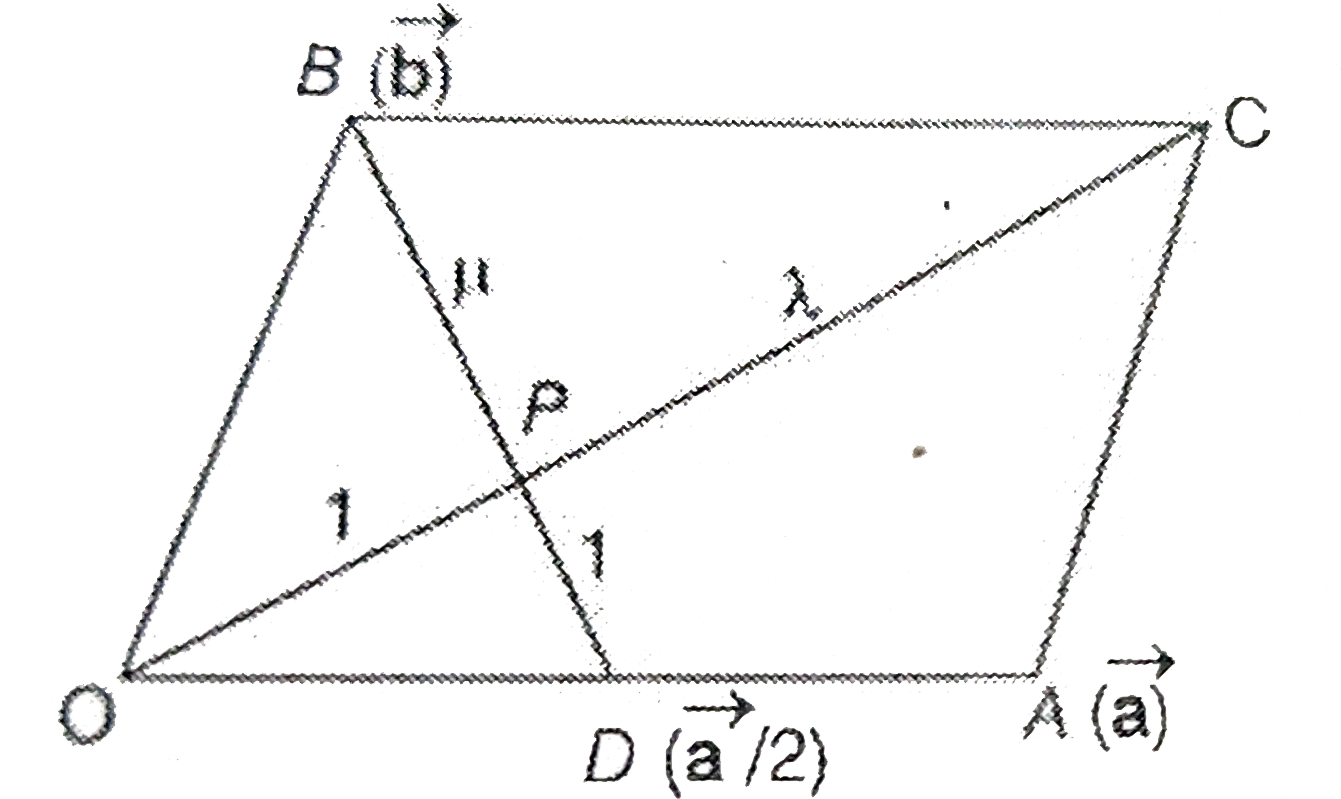
and −−→OD=→a2
−−→CO and −−→BD meets at P.
∴−−→OP=λ.0+1(→a+→b)λ+1 [along −−→OC]
⇒−−→OP=→a+→bλ+1 ......(i)
Again −−→OP=μ(→a2)+1(→b)μ+1 [along −−→BD]
⇒−−→OP=μ→a+2→b2(μ+1) .........(ii)
From Eqs . (i) and (ii)
→a+→bλ+1=μ→a+2→a2(μ+1)⇒1λ+1=μ2(μ+1) and 1λ+1=1μ+1
On solving we get μ=λ=2
Thus required ratio is 2:1
Topper's Solved these Questions
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - VECTOR ALGEBRAEXERCISE - Scalar Product of two vectors (Interger Answer Type Questions )2videos
VECTOR ALGEBRA
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - VECTOR ALGEBRAEXERCISE - Vector Product of Two Vectors (Objective Questions I)12videos
VECTOR ALGEBRA
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - VECTOR ALGEBRAEXERCISE - Scalar Product of two vectors (Fill in the Blanks)3videos
VECTOR ALGEBRA
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - TRIGONOMETRICAL RATIOS AND IDENTITIESEXERCISE - HEIGHT AND DISTANCE10videos
TRIGONOMETRICAL RATIOS AND IDENTITIES
Similar Questions
Let OACB be a parallelogram with O at the origin andOC a diagonal. Let D be the midpoint of OA. using vector methods prove that BDandCO intersect in the same ratio. Determine this ratio.
View SolutionABCD is a parallelogram whose diagonals AC and BD intersect at O. A Line through O intersects AB at P and DC at Q. Prove that ar(△POA)=ar(△QOC).
View Solution
Knowledge Check
- Question 1 - Select One
Let ABCD be a parallelogram whose diagonals intersect at P and O be the origin, then OA+OB+OC+OD equals
AOPB2OPC3OPD4OP - Question 2 - Select One
Let ABCD be a parallelogram whose diagonals intersect at P and let O be the origin. What is −−→OA+−−→OB+−−→OC+−−→OD equal to
A2−−→OPB4−−→OPC6−−→OPD8−−→OP
Let ABCD be as parallelogram. If →a, →b, →c be the position vectors of A, B, C respectively with reference to the origin O, find the position vector of D reference to O.
View SolutionABCD is a parallelogram whose diagonals AC and BD intersect at O. A line through O intersects AB at P and DC at Q. Prove that ar (ΔPOA)= ar (ΔQOC).
View SolutionThe diagonals of a parallelogram ABCD intersect at OA line through O intersects AB at XandDC at Y Prove that OX=OY
View SolutionABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that: ar (ADO)=AR (CDO) ar ( ABP)= ar ( CBP)
View SolutionO is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(OAB)=ar(OBC)
View SolutionThe diagonals of a parallelogram ABCD intersect at O.A line through O intersects AB at X and DC at Y. Prove that OX=OY.
View Solution

