As seen in two spheres of mass m and a third sphere of mass M form an equilateral triangle, and a fourth sphere of mass m4 is at the center of the triangle. The net gravitational force on that central sphere from the three other spheres is zero. (a) What is M in terms of m? (b) If we double the value of m4 what then is the magnitude of the net gravitational force on the central sphere?
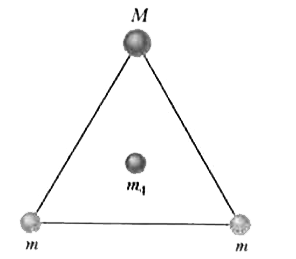
(a) m = M, (b) The net force is still zero.
Topper's Solved these Questions
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
16 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
7 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - CHECKPOINT
5 Videos
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Practice questions(Integers)
4 Videos
- HEAT-MEASUREMENT AND TRANSFERBOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - PRACTICE QUESTIONS( INTEGER TYPE)
5 Videos
Similar Questions
Two spheres of masses 16 kg and 4 kg are separated by a distance 30 m on a table. Then, the distance from sphere of mass 16 kg at which the net gravitational force becomes zero is
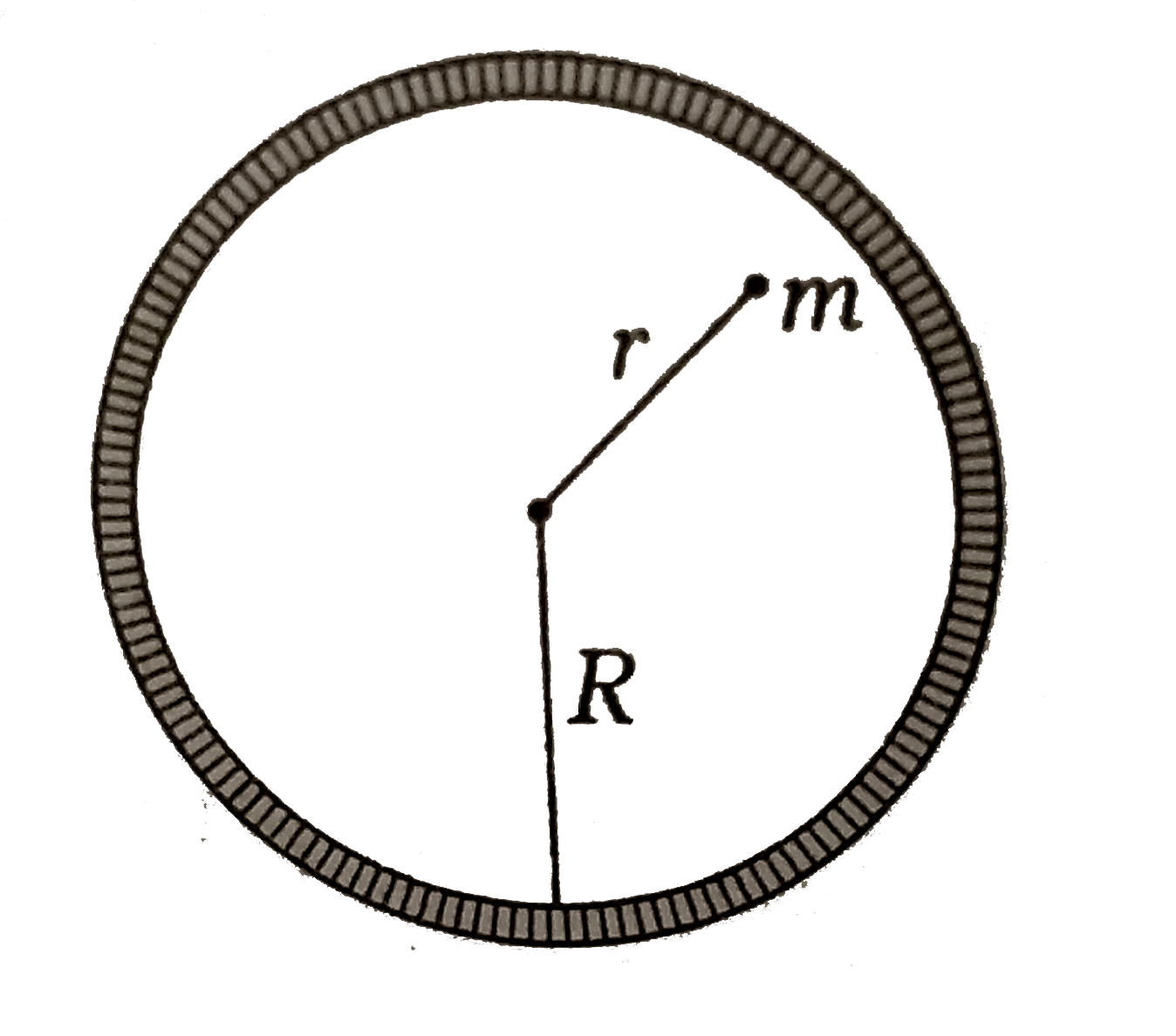
View SolutionA mass m is placed inside a hollow sphere of mass M as shown in figure. The gravitaional force on mass m is
View Solution
Knowledge Check
Two spheres of masses 16 kg and 4 kg are separated by a distance 30 m on a table. Then, the distance from sphere of mass 16 kg at which the net gravitational force becomes zero is
A10 mB20 mC15 mD5 mA mass m is placed inside a hollow sphere of mass M as shown in figure. The gravitaional force on mass m is
 AGMmR2BGMmr2CGMm(R−r)2Dzero
AGMmR2BGMmr2CGMm(R−r)2DzeroA mass m is placed in the cavity inside hollow sphere of mass M as shown in the figure. The gravitational force on m is
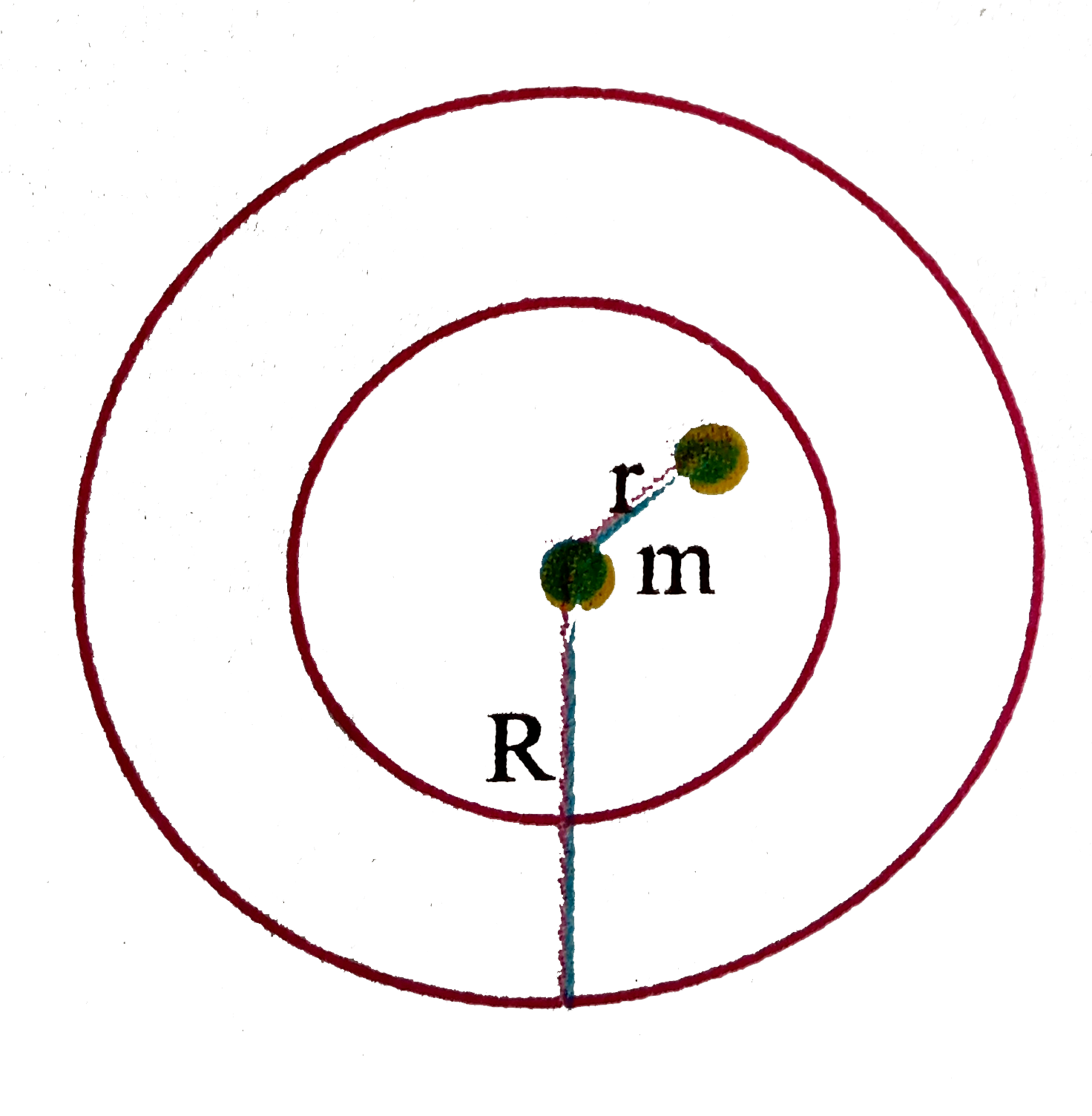 AGMmR2BGMmr2CGMm(R−r)2Dzero
AGMmR2BGMmr2CGMm(R−r)2Dzero
The gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View SolutionA uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The center of the ring is at a distance √3a from the center of the sphere. Find the gravitational force exerted by the sphere on the ring.
View SolutionA uiform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and same radius R. The centre of the sphere. The gravitational atraction between the sphere and the ring is
View SolutionThree uniform spheres each of mass m and diameter D are kept in such a way that each touches the other two, then magnitudes of the gravitational force on any one sphere due to the other two is
View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View Solution
