Find the equation of the circle having radius 5 and which touches line 3x+4y−11=0 at point (1, 2).
As shown in the figure, the two circles touch the line 3x+4y−11=0 at point (P(1,2).
∴ Centre lies on the line perpendicular to the tangent at P at distance 5 from it on either side.
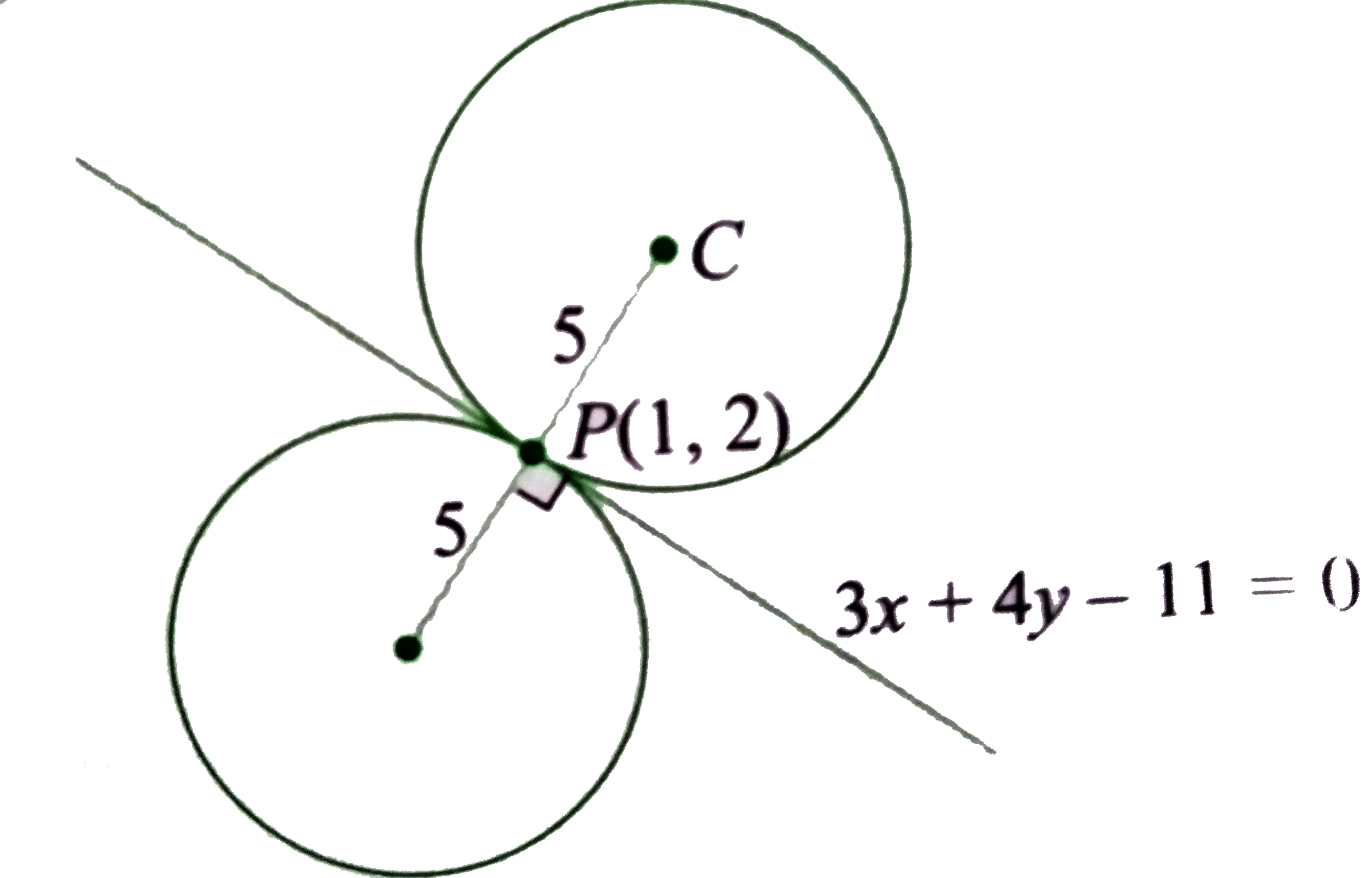
Slope of given tangent line is −34
Thus, the slope of CP is 43.
∴tanθ=43
∴Centre, C≡(1±5cosθ,2±5sinθ)
∴C≡(1±535,2±545)
∴C≡(4,6) or (−2,−2)
Therefore, equations of circles are
(x−4)2+(y−6)2=25
or (x+2)2+(y+2)2=25
Topper's Solved these Questions
Similar Questions
Find the equation of the circle having radius 5 and touching the line 3x−4y+5=0 at the point (1,2).
View SolutionFrom a point P, tangents drawn to the circle x2+y2+x−3=0,3x2+3y2−5x+3y=0and4x2+4y2+8x+7y+9=0 are of equal lengths. Find the equation of the circle through P, which touches the line x+y=5 at the point (6,−1).
View Solution
Knowledge Check
- Question 1 - Select One
Equation of circle having radius 5, and touching X-axis at (-1,0), is
Ax2+y2±2x+10y−1=0Bx2+y2±2x−10y+1=0Cx2+y2+2x+10y±1=0Dx2+y2+2x±10y+1=0
Find the equation of the circle having centre at (3,−4) and touching the line 5x+12y−12=0.
View SolutionFind the equation of the circle whose radius is 5and which touches the circle x2+y2−2x−4y−20=0 externally at the point (5,5).
View SolutionFind the equation of the circle having
centre at (3,2), and touching the line
4x+3y−8=0 .View SolutionFind the equation of a circle with centre (1,-3) and touches the line 2x-y-4=0.
View SolutionThe equation of the circle whose radius is 5 and which touches the circle
x2+y2±2x−4y−20=0 at the point (5,5) isView SolutionFind the equation of the circle passing through the point (−2,1) and touching the line 3x−2y−6=0 at the point (4,3).
View SolutionFind the equation of circles with radius 12 and touching the circle x2+y2=25 at the point (3,4)
View Solution

