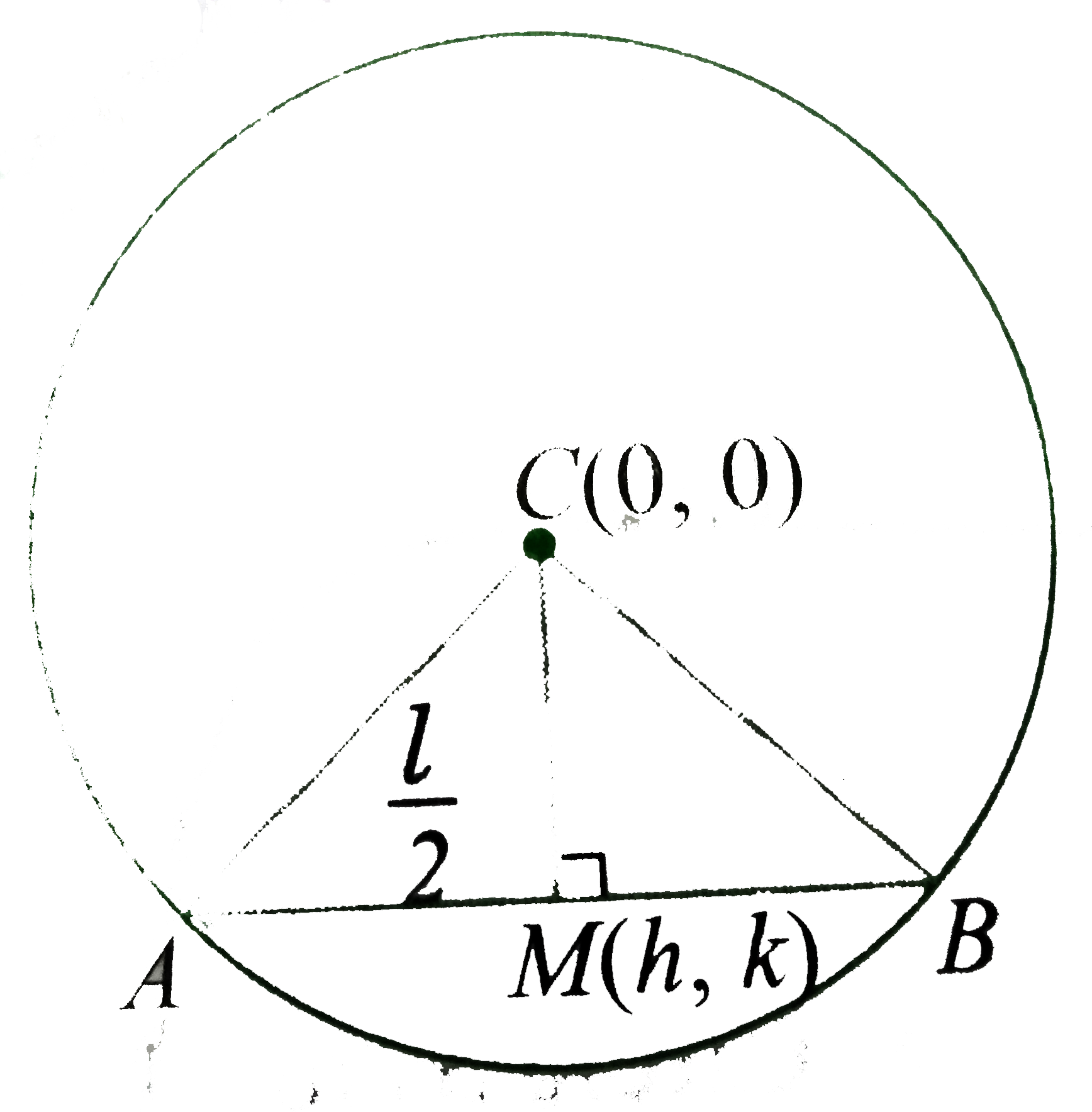
Find the locus of the midpoint of the chords of circle $x^{2} + y^{2} = a^{2}$ having fixed length l.

Video Solution

Text Solution

Verified by Experts

As shown in the figure, AB is one of the variable chords having length l.
Let the midpoint of AB is M(h,k) .
The foot of perpendicular from centre C on AB is M.
In right angles triangled CMA, we have
$A C^{2} = C M^{2} + A M^{2}$
$∴ a^{2} = (h^{2} + k^{2}) + {(\frac{l}{2})}^{2}$
Hence, equation of required locus is $x^{2} + y^{2} = a^{2} - \frac{l^{2}}{4}$ .

Updated on:21/07/2023

The locus of the mid -point of the chords of a circle $x^{2} + y^{2} = 4$ ,which subtends a right angle at the centre , is
A $x + y = 2$
B $x^{2} + y^{2} = 1$
C $x^{2} + y^{2} = 2$
D $x - y = 0$
The locus of the midpoints of chords of length 2d of $x y = c^{2}$ is :
A $(x^{2} + y^{2}) (x y - c^{2}) = d^{2}$
B $(x^{2} + y^{2}) (x y - c^{2}) = d^{2} x y$
C $(x^{2} + y^{2}) (x y - c^{2}) = x y$
D $2 (x y - c^{2}) = d^{2}$
Locus of the mid-points of the chords of the circle $x^{2} + y^{2} = a^{2}$ which are always at a constant distance from the centre is
Aparabola
Bellipse
Ccircle
Dnone