If from any point $P$ on the circle $x^{2} + y^{2} + 2 g x + 2 f y + c = 0,$ tangents are drawn to the circle $x^{2} + y^{2} + 2 g x + 2 f y + c {sin}^{2} α + (g^{2} + f^{2}) {cos}^{2} α = 0$ , then find the angle between the tangents.

Video Solution

Text Solution

Verified by Experts

Given circles are $x^{2} + y^{2} + 2 g x + 2 f y + c = 0$ (1)
and $x^{2} + y^{2} + 2 g x + 2 f y + c {sin}^{2} α + (g^{2} + f^{2}) {cos}^{2} α = 0$ (2)

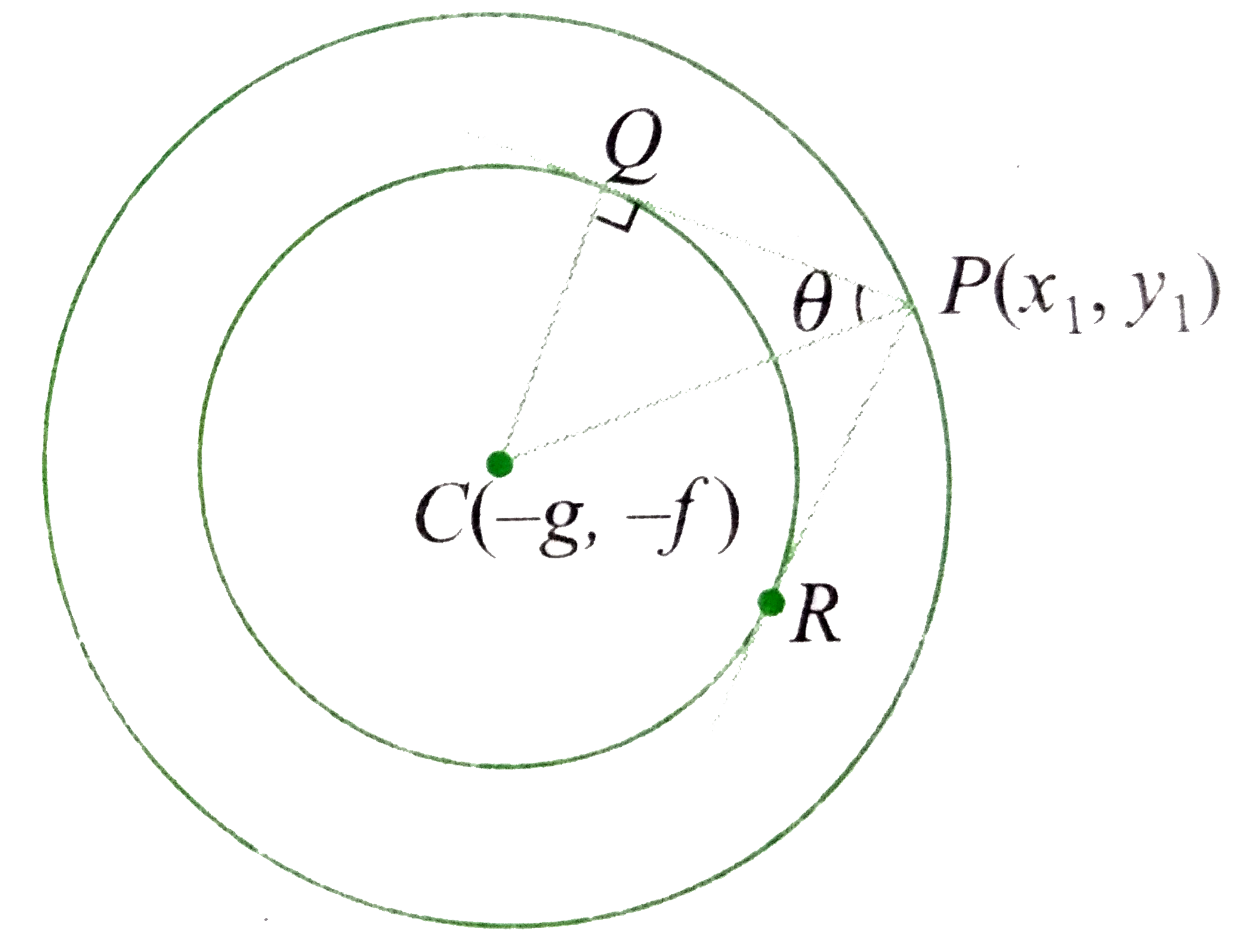
Let $P (x_{1}, y_{1})$ be a point on the circle (1).
$∴ x_{1}^{2} + y_{1}^{2} + 2 g x_{1} + 2 f y_{1} + c = 0$ (3)
The length of the tangent drawn from $P (x_{1}, y_{1})$ to the circle (2) is
$P Q = \sqrt{x_{1}^{2} + y_{1}^{2} + 2 g x_{1} + 2 f y_{1} + c {sin}^{2} α + (g + f^{2}) {cos}^{2} α}$
$= \sqrt{- c + c {sin}^{2} α + (g^{2} + f^{2}) {cos}^{2} α})$ (Using (1))
$= (\sqrt{g^{2} + f^{2} - c}) cos α$
The radius of the circle (2) is
$C Q = (\sqrt{g^{2} + f^{2} - c {sin}^{2} α - (g^{2} + f^{2}) {cos}^{2} α}$
$= (\sqrt{g^{2} + f^{2} - c}) sin α$
In $Δ C P Q$
$tan θ = \frac{C Q}{P Q} = \frac{\sqrt{g^{2} + f^{2} - c} sin α}{\sqrt{g^{2} + f^{2} - c} cos α} = tan α$
$∴ θ = α$
Therefore, angle between tangents is $2 α$ .

Updated on:21/07/2023

If from any point $P$ on the circle $x^{2} + y^{2} + 2 g x + 2 f y + c = 0,$ tangents are drawn to the circle $x^{2} + y^{2} + 2 g x + 2 f y + c {sin}^{2} α + (g^{2} + f^{2}) {cos}^{2} α = 0$ , then find the angle between the tangents.
A $α$
B $2 α$
C $α / 2$
Dnone
If two tangents are drawn from a point to the circle $x^{2} + y^{2} = 32$ to the circle $x^{2} + y^{2} = 16$ , then the angle between the tangents is :
A $\frac{π}{4}$
B $\frac{π}{3}$
C $\frac{π}{2}$
D $\frac{π}{6}$
If two tangents are drawn from a point to the circle $x^{2} + y^{2} = 32$ to the circle $x^{2} + y^{2} = 16$ , then the angle between the tangents is
A $\frac{- π}{4}$
B $\frac{π}{3}$
C $\frac{π}{2}$
D $\frac{π}{6}$