Find the equation of the tangent at the endpoints of the diameter of circle (x−a)2+(y−b)2=r2 which is inclined at an angle θ with the positive x-axis.
Video Solution
Text Solution
Diameter makes an angle θ with x-axis.
So, the slope of diameter is tanθ
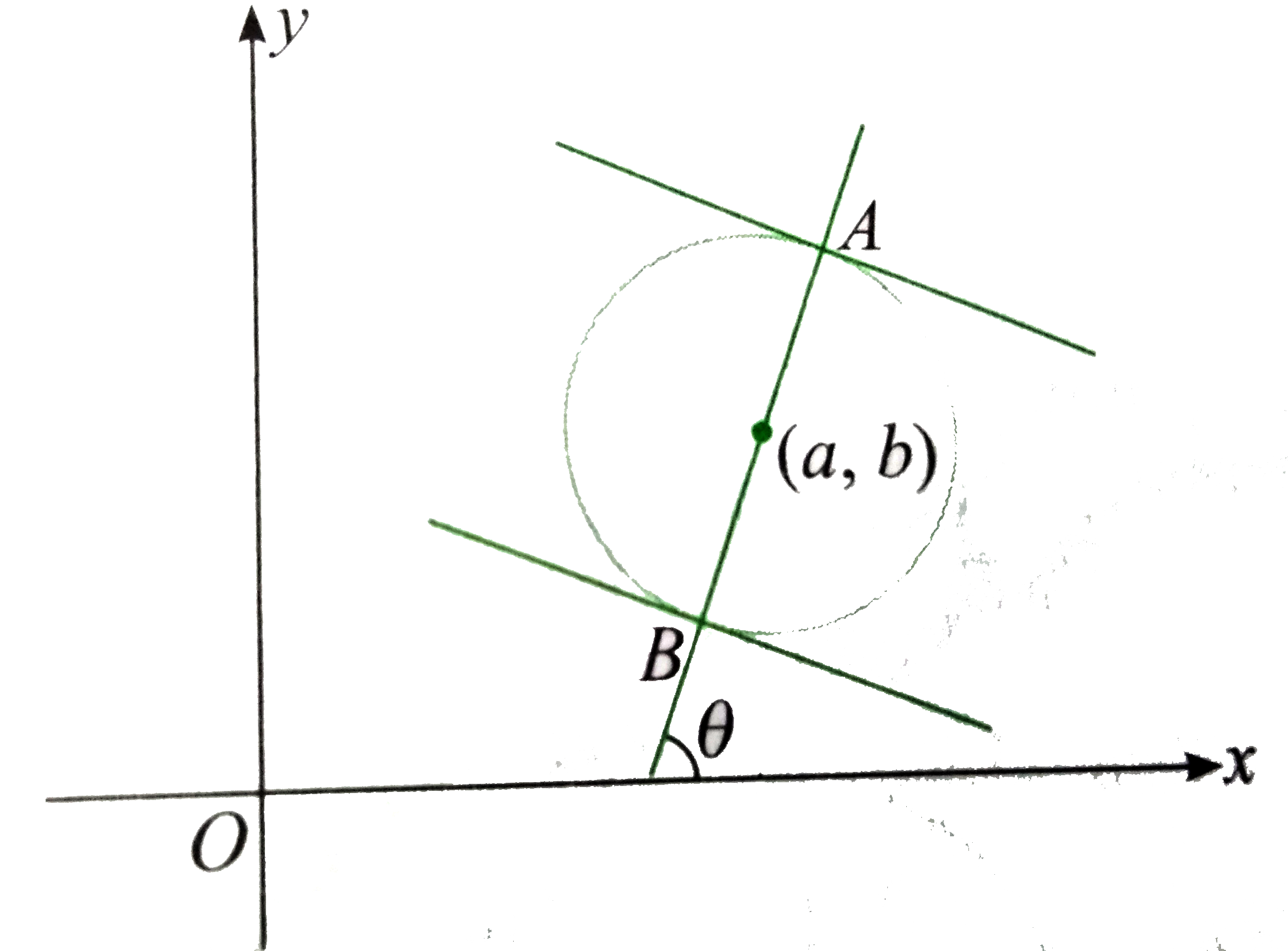
Let this diameter meet the circle at points A and B.
Thus, the coordinates of A and B are given by (a±rcosθ,b±rsinθ)
Therefore, equations of tangents at points A and B are given by
(x−a)(a±rcosθ−a)+(y−b)(b±rsinθ−b)=r2
or ±(x−a)cosθ±r(y−b)sinθ=r
or (x−a)cosθ+(y−b)sinθ=±r
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The points of contact of tangents to the circle x2+y2=25 which are inclined at an angle of 30∘ to the x-axis are
A(±5/2,±1/2)B(±1/2,±5/2)C(±5/2,±1/2)Dnone of these - Question 2 - Select One
The equation of a tangent to the parabola, x2=8y, which makes an angle θ with the positive direction of x-axis, is:
Ay=xtanθ+2cotθBy=xtanθ+2tanθCx=ycotθ+2tanθDy=xtanθ−2cotθ
Find the equations of the common tangents to the circle x2+y2=8 and the parabola y2=16x.
View SolutionFind the equation of the tangent to the circle x2+y2−30x+6y+109=0 at (4,−1)
View SolutionFind the equations of the tangents to the hyperbola 3x2−4y2=12 , which are inclined at an angle 60∘ to x-axis.
View SolutionFind the equation of the tangent to the parabola y2−6x+8y−6=0 which is inclined at an angle of 45∘ to the x-axis.
View SolutionFind the locus of point of intersection of tangent to the parabola y2=4ax which are inclined at an angle θ to each other.
View SolutionThe equation of the common tangent touching the parabola y2=4x and the circle (x−3)2+y2=9 above the x-axis is
View Solution

