Find the locus of the center of the circle touching the circle $x^{2} + y^{2} - 4 y = 4$ internally and tangents on which from (1, 2) are making of $60^{0}$ with each other.

Video Solution

Text Solution

Verified by Experts

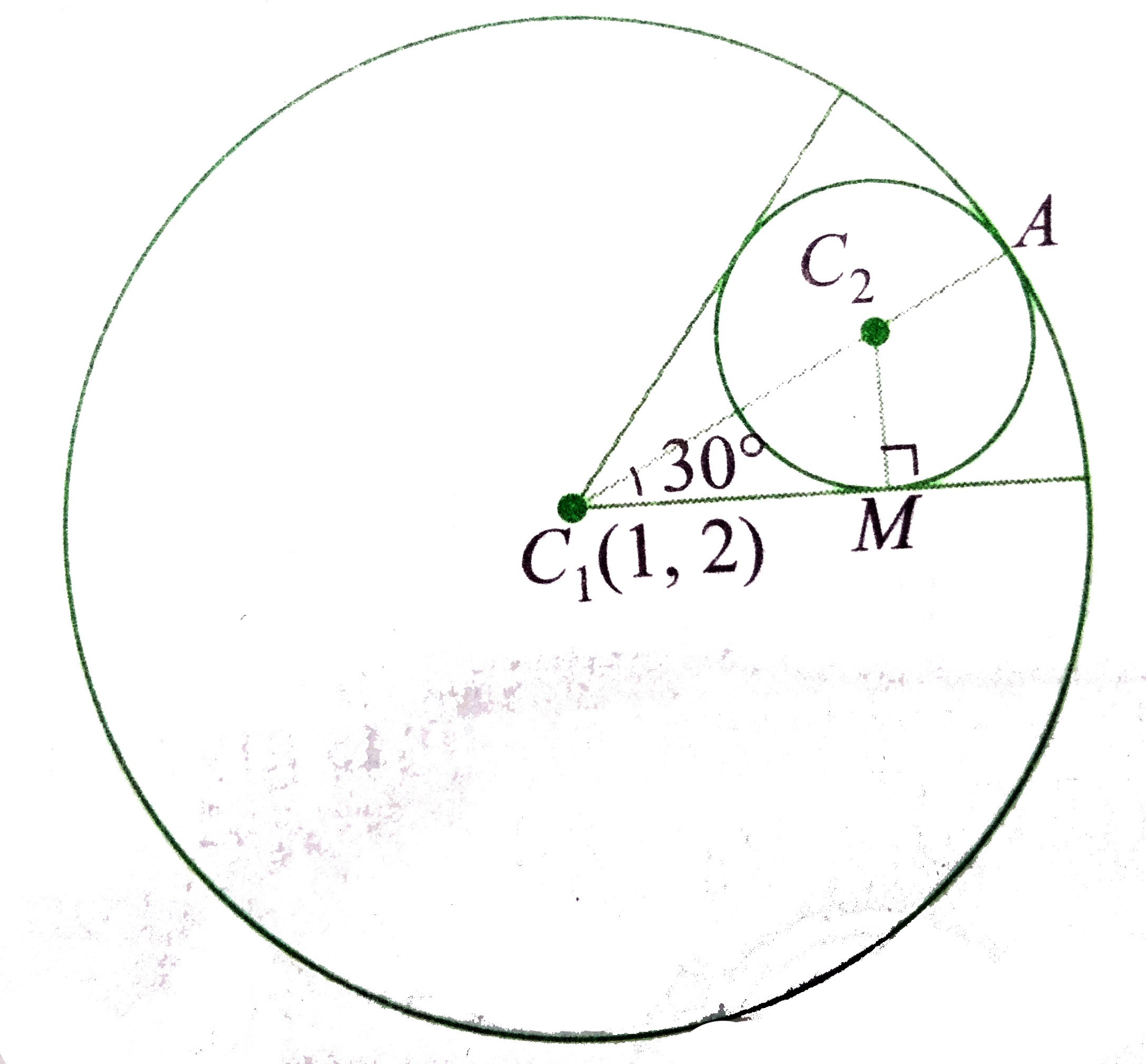
Given circle is $x^{2} + y^{2} - 4 y - 2 x - 4 = 0$
Centre is $C_{1} (1, 2)$ and radius is $r_{1} = \sqrt{{(- 2)}^{2} + {(- 1)}^{2} - (- 4)} = 3$ .
Let the centre of the variable circles touching given circle be $C_{2} (h, k)$ .
Angle between tangents drawn from $C_{1} (1, 2)$ to variable circle is $60^{\circ}$ .
In triangle $C_{1} M C_{2}$ .
${\sin 30}^{\circ} = \frac{C_{2} M}{C_{1} C_{2}}$
$\Rightarrow {\sin 30}^{\circ} = \frac{C_{2} A}{C_{1} C_{2}}$
$\Rightarrow \frac{1}{2} = \frac{C_{1} A - C_{1} C_{2}}{C_{1} C_{2}} = \frac{3 - C_{1} C_{2}}{C_{1} C_{2}}$
$\Rightarrow C_{1} C_{2} = 2$
$\Rightarrow \sqrt{{(h - 1)}^{2} + {(k - 2)}^{2}} = 2$
Therefore, required locus is ${(x - 1)}^{2} + {(y - 2)}^{2} = 4$ .

Updated on:21/07/2023

Find the radius and centre of the circle of the circle $x^{2} + y^{2} + 2 x + 4 y - 1 = 0$ .
A $\sqrt{6}$ and $(- 1, - 2)$
B $\sqrt{2}$ and $(1, 2)$
C $\sqrt{7}$ and $(- 1, - 3)$
Dnone of these
The locus of centre of circle which touches the circle $x^{2} + y^{2} = 1$ and $y -$ axis in 1st quadrant is
A $y^{2} = 2 x - 1$
B $x^{2} + 1 = 2 y$
C $y^{2} = 2 x + 1$
D $x^{2} - 1 = 2 y$