Lines $5 x + 12 y - 10 = 0$ and $5 x - 12 y - 40 = 0$ touch a circle C1 of diameter 6. If the centre of C1, lies in the first quadrant then the equation of the circle C2, which is concentric with C1, and cuts intercepts of length 8 on these lines is

Video Solution

Text Solution

Verified by Experts

According to the question, circles are drawn as shown in the figure.

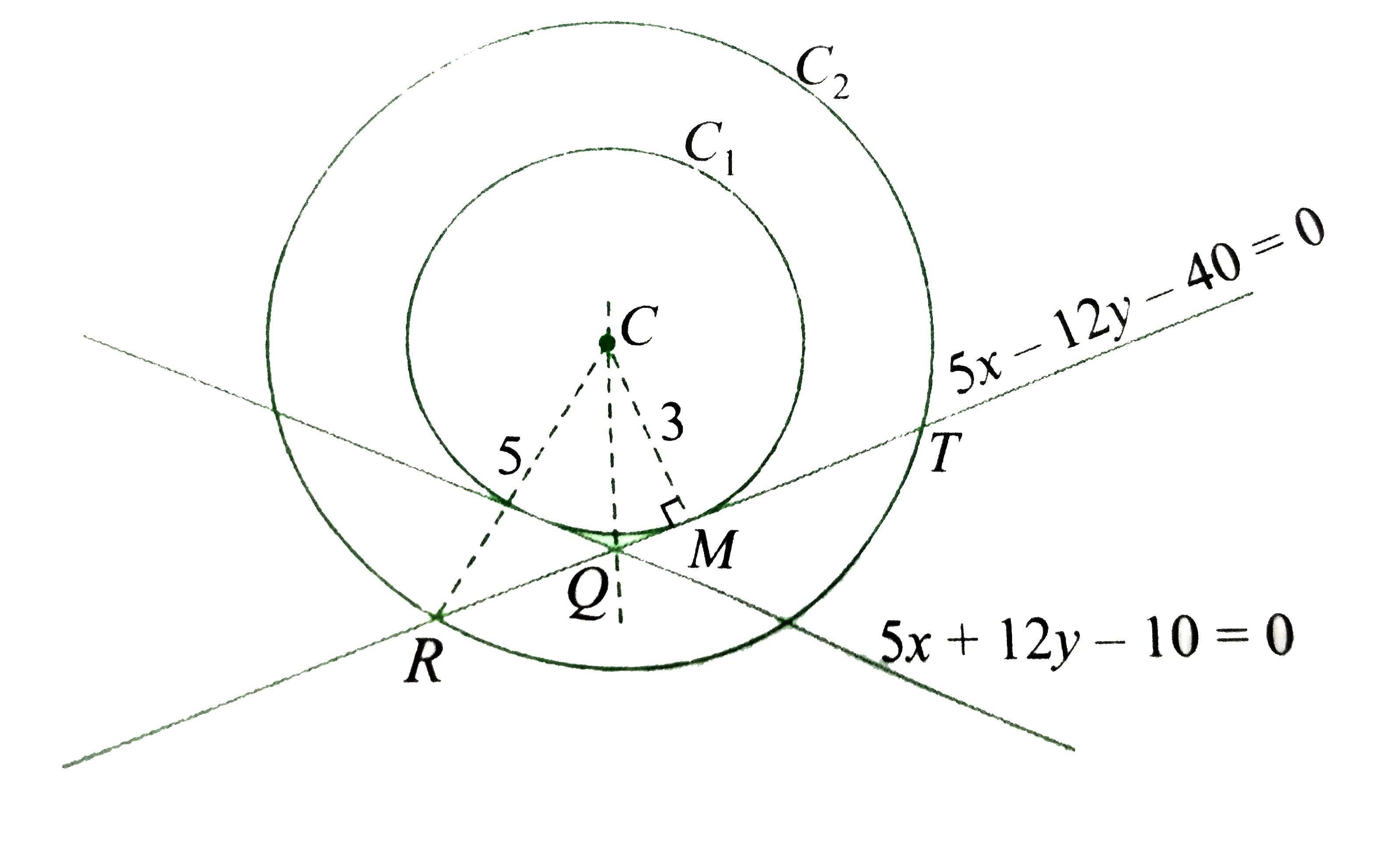
Centre of the circles lies on one of the angle bisectors of the given lines.
$\frac{5 x + 12 y - 10}{13} = \pm \frac{5 x - 12 y - 40}{13}$
or $24 y = - 30$ and $10 x = 50$
But centre lies in first quadrant.
So, for centre , $x = 5$ .
Distance of centre (C(5,y) from the line $5 x + 12 y - 10 = 0$ is 3.
$∴ \frac{5 (5) + 12 y - 10}{13} = \pm 13$
$∴ y = 2$ (As centre lies in first quadrant)
Sol, centre is (5,2).
Alsok, in right angles triangle CMR, $C R = 5 ($ as $R M = 4)$ .
Hence, equation of circle is ${(x - 5)}^{2} - {(y - 2)}^{2} = 5^{2}$ .

Updated on:21/07/2023

|

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Radius of the circle with centre (3,1) and cutting a chord of length 6 on the line $2 x + 5 y + 18 = 0$ is
A6
B7
C $\sqrt{38}$
D $2 \sqrt{5}$

CENGAGE-CIRCLE -JEE Advanced (Single Correct Answer Type)

Home
Ask Doubt
Profile