The locus of the centers of the circles such that the point (2, 3) is the mid point of the chord $5 x + 2 y = 16$ is

A

$2 x - 5 y + 11 = 0$

B

$2 x + 5 y - 11 = 0$

C

$2 x + 5 y + 11 = 0$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:1

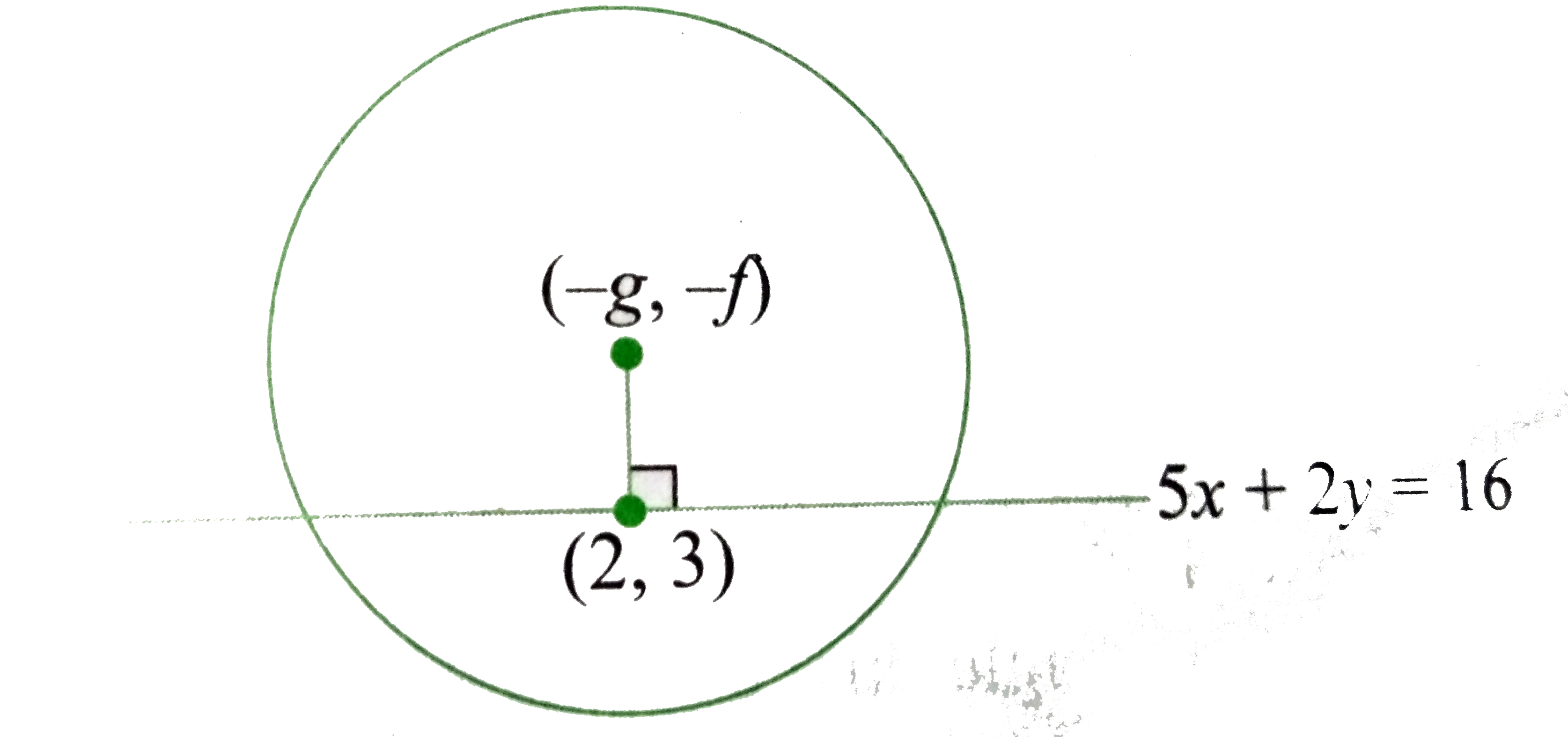
Slope of the given line $= - \frac{5}{2}$
$∴ (- \frac{5}{2}) (\frac{3 + f}{2 + g}) = - 1$
or $15 + 5 f = 4 + 2 g$
Therefore, the locus is $2 x - 5 + 11 = 0$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The locus of the mid points of the chords passing through a fixed point $(α, β)$ of the hyperbola $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ is
Aa circle with centre $(\frac{α}{2}, \frac{β}{2})$
Ban ellips with center $(\frac{α}{2}, \frac{β}{2})$
C ${(x^{2} + y^{2})}^{2} = a^{2} (x^{2} - y^{2})$
D $2 {(x^{2} - y^{2})}^{2} = 3 a^{2} (x^{2} + y^{2})$
Question 2 - Select One or More
The locus of the point of intersection of the tangents at the extermities of a chord of the circle $x^{2} + y^{2} = b^{2}$ which touches the circle $x^{2} + y^{2} - 2 b y = 0$ passes through the point
A $(0, \frac{b}{2})$
B(0,b)
C(b,0)
D $(\frac{b}{2}, 0)$
Question 3 - Select One
If from the origin a chord is drawn to the circle $x^{2} + y^{2} - 2 x = 0$ , then the locus of the mid point of the chord has equation
A $x^{2} + y^{2} + x + y = 0$
B $x^{2} + y^{2} + 2 x + y = 0$
C $x^{2} + y^{2} - x = 0$
D $x^{2} + y^{2} - 2 x + y = 0$

CENGAGE-CIRCLE -Exercise (Single)

Home
Ask Doubt
Profile