The line 2x−y+1=0 is tangent to the circle at the point (2, 5) and the center of the circle lies on x−2y=4 . Then find the radius of the circle.
3√5
5√3
2√5
5√20
The correct Answer is:A
2x−y+1=0 is a tangent.
Slope of line OA=−12
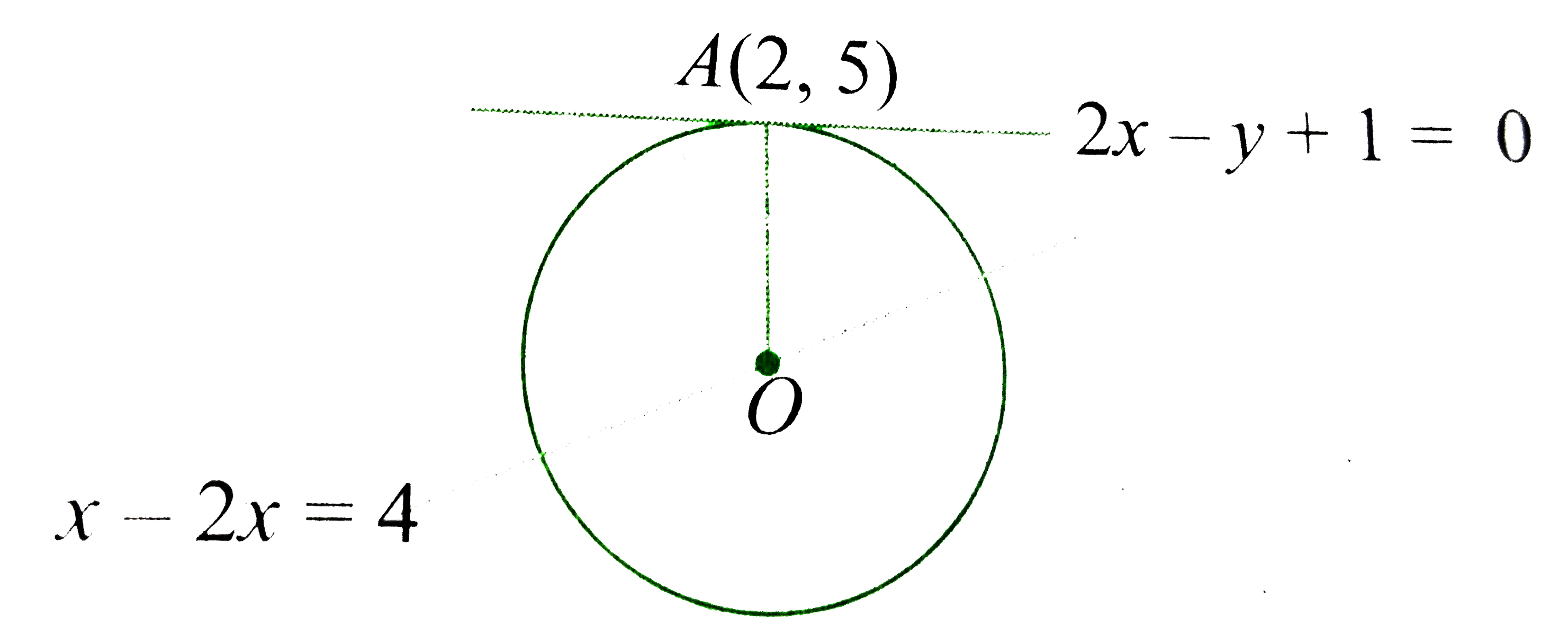
The equation of OA is
(y−5)=−12(x−2)
or x+2y=12
Therefore , intersection with x−2y=4 will give the coordinates of centre as (8,2) . Hence,
r=OA=√(8−2)2+(2−5)2=3√5
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.6
5 Videos
- BINOMIAL THEORMBOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank
31 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
Similar Questions
The line 2x - y + 1 = 0 is tangent to the circle at the point (2,5) and the centre of the circles lies on x-2y = 4. The radius of the circle is :
View SolutionThe line 2x−y+1=0 is tangent to the circle at the point (2,5) and the centre of the circles lies on x−2y=4. The radius of the circle is
View Solution
Knowledge Check
The line 2x−y+1=0 is tangent to the circle at the point (2, 5) and the centre of the circle lies on x−2y=4. The square of the radius of the circle is
A45B75C20D50The line 2x−y+1=0 touches a circle at the point (2, 5) and the centre of the circle lies on x−2y=4. The diameter (in units) of the circle is
A6√5B10√3C4√5D10√2A circle touches the lines x−y−1=0andx−y+1=0. the centre of the circle lies on the line
Ax+y−1=0Bx+y+1=0Cx−y=0Dnone of these
The line 2x−y+1=0is tangent to the circle at the point (2,5) and the centre of the circles lies on x−2y=4 The radius of the circle is:
View SolutionThe line 2x−y+1=0 is tangent to the circle at the point (2, 5) and the center of the circle lies on x−2y=4. The radius of the circle is 3√5 (b) 5√3 (c) 2√5 (d) 5√2
View SolutionIf the line 2x−y+1=0 touches the circle at the point (2,5) and the centre of the circle lies in the line x+y−9=0. Find the equation of the circle.
View SolutionThe line 5x−y=3 is a tangent to a circle at the point (2,7) and its centre is on theline x+2y=19. Find the equation of the circle.
View SolutionIf the line y=2-x is tangent to the circle S at the point P(1,1) and circle S is orthogonal to the circle x2+y2+2x+2y−2=0 then find the length of tangent drawn from the point (2,2) to the circle S
View Solution
