Find the perimeter of the shaded region in the figure,if ABCD is a square of side 14 cm and APB and CPD are semicircles.

The correct Answer is:72cm
Perimeter of the shaded region
= perimeter of semicircle DPC + perimeter of semicircle APB+AD+BC
={(227×7)+(227×7)+14+14}cm=(22+22+28)cm=72cm
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - Multiple Choice Questions (Mcq)26videos
AREA OF CIRCLE, SECTOR AND SEGMENT
- BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - Test Yourself19videos
AREA OF CIRCLE, SECTOR AND SEGMENT
- BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - EXERCISE1videos
AREA OF CIRCLE, SECTOR AND SEGMENT
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)30videos
ARITHMETIC PROGRESSION
Similar Questions
Find the area of the shaded region in the given figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
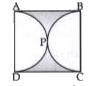 View Solution
View SolutionFind the area of the shaded region of the given figure, if ABCD is a square of side 14 cm and APD and BPC are semi-circles. ( Takeπ=227)
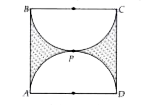 View Solution
View SolutionFind the perimeter of the shaded region if ABCD is a square of side 14 cm and APB and CPD are semicircles
View SolutionFind the area of the shaded region in figure, if ABCD is a square of side 7 cm. and APD and BPC are semi-circles
View SolutionFind the area of the shaded region in Fig. 12.21, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
View SolutionFind the area of the shaded region in figure where ABCD is a square of side 14 cm.
 View Solution
View SolutionFind the area of the shaded region in Fig. 15.49, if ABCD is a square of side 14 cm and APD and BPC are semi-circles. (FIGURE)
View SolutionFind the area of the shaded region in Fig where ABCD is a square of side 14 cm.
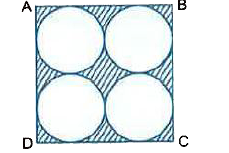 View Solution
View SolutionFind the area of the shaded region as shown in figure, where ABCD is square of side 14 cm.
View SolutionFind the area of the shaded region in Fig. 12.16, where ABCD is a square of side 14 cm.
View Solution

