In the given figure, the shape of the top of a table is that of a sector of a circle with centre O and ∠AOB=90∘. If AO=OB=42cm then find the perimeter of the top of the table.
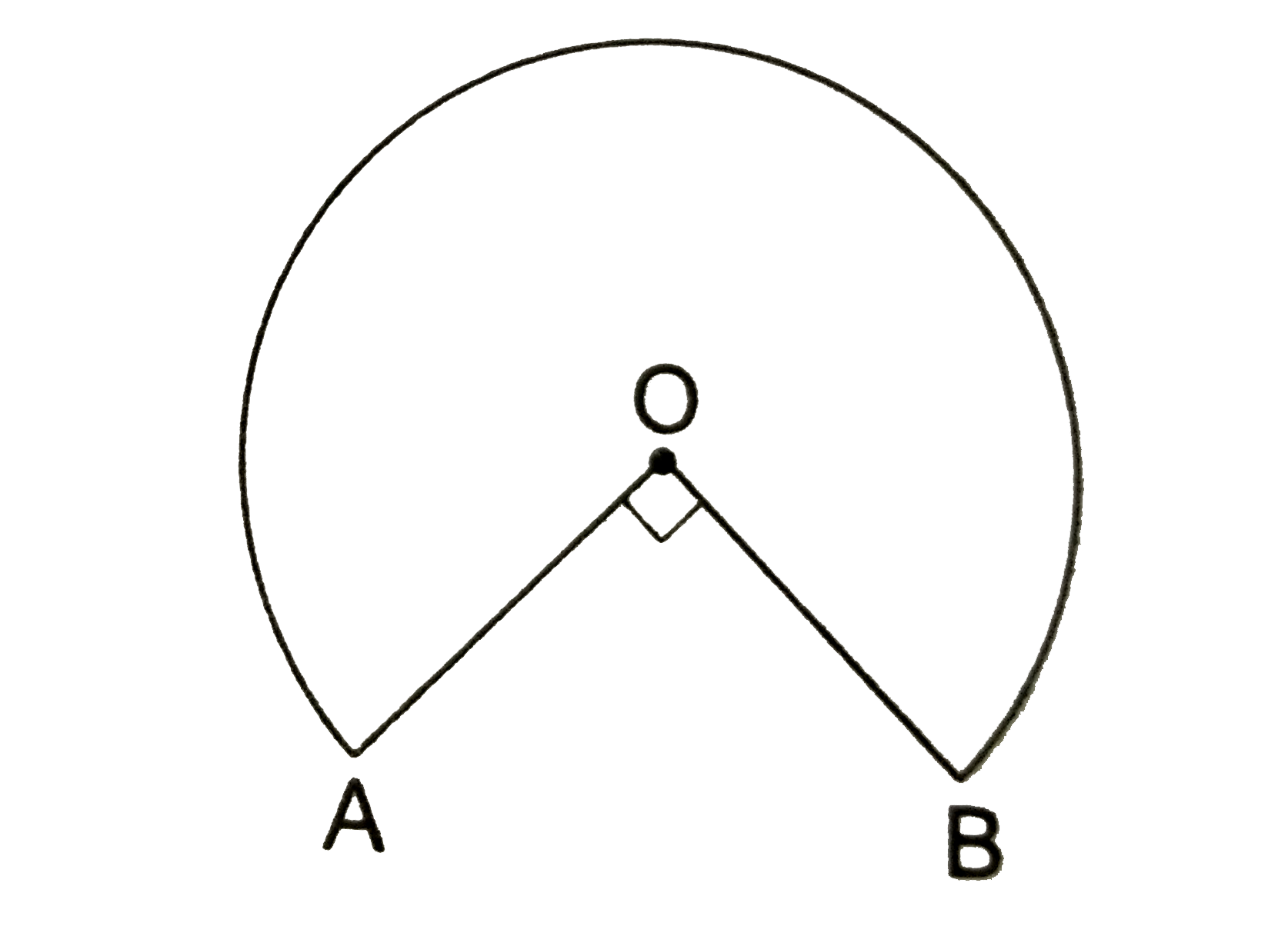
The correct Answer is:282cm
Required perimeter = (circumference − arc AB) +(OA+OB)
={(2×227×42)−(2×227×42×90360)+(42+42)}cm
=(264−66+83)cm=282cm
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - Multiple Choice Questions (Mcq)26videos
AREA OF CIRCLE, SECTOR AND SEGMENT
- BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - Test Yourself19videos
AREA OF CIRCLE, SECTOR AND SEGMENT
- BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - EXERCISE1videos
AREA OF CIRCLE, SECTOR AND SEGMENT
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)30videos
ARITHMETIC PROGRESSION
Similar Questions
In the given figure, O is the centre of the circle.

Shade sectors OAC and OPB.View SolutionFind the area of a sector of a circle of radius 7 cm and central angle 90∘.
View SolutionIn the given figure,AB and CDare equal chords of a circle with centre O .Prove that ∠AOB≅∠COD and ∠AOB=∠COD
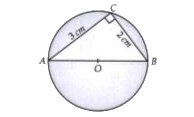
View SolutionIn the given figure, AOB is a diameter of a circle with centre O. Find tan A tan B.
 View Solution
View SolutionAB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm. Find the area of sector of the circle formed by chord AB .
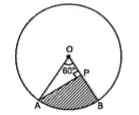
View SolutionIn the given figure, AOB is a sector of angle 60∘ of a circle with centre O and radius 17 cm. If AP ⊥ OB and AP = 15 cm, find the area of the shaded region.
 View Solution
View SolutionIn the adjoining figure, O is the centre of the circle. AB is an arc of the circle and ∠AOB=80∘. Find ∠ACB.
 View Solution
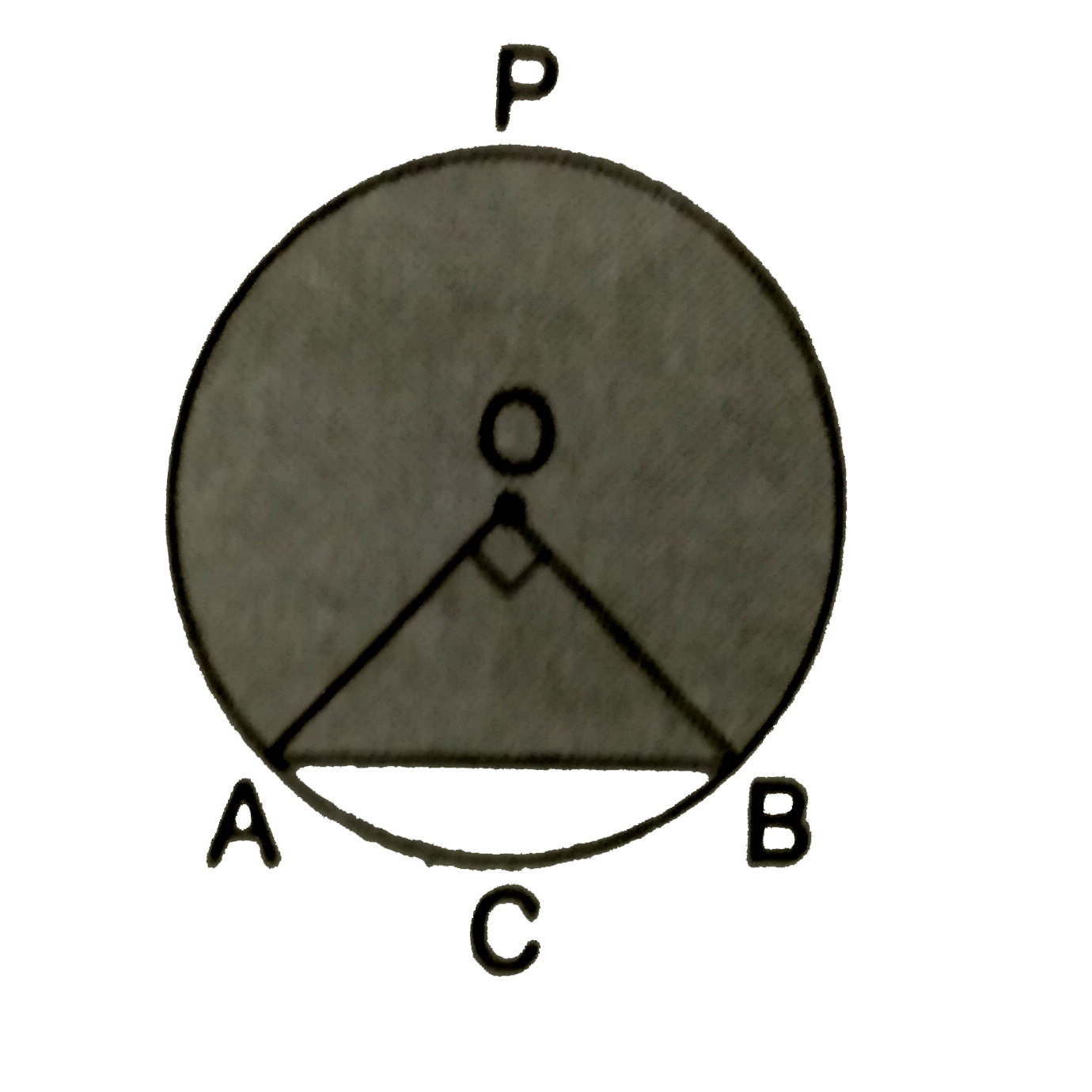
View SolutionFind the area of the major segment APB of a circle of radius 35 cm and ∠AOB=90∘ as shown in the given figure.
 View Solution
View SolutionIn the given figure, AB and CD are two equal chords. If O is the centre of the circle , ∠AOB=120∘, then find ∠OCD.
 View Solution
View SolutionIn the given figure PA and PB are tangents to a circle with centre O.If∠APB=(2x+3)∘ and∠AOB=(3x+7)∘ then, find the value of x.
View Solution

