In a circle of radius 7cm, a square ABCD is inscribed. Find the area of the cirle which is outside the square.
The correct Answer is:63cm2
Diagonal of the square =(2×7)cm=14cm
Area of the square =12d2=(12×14×14)cm2=91cm2
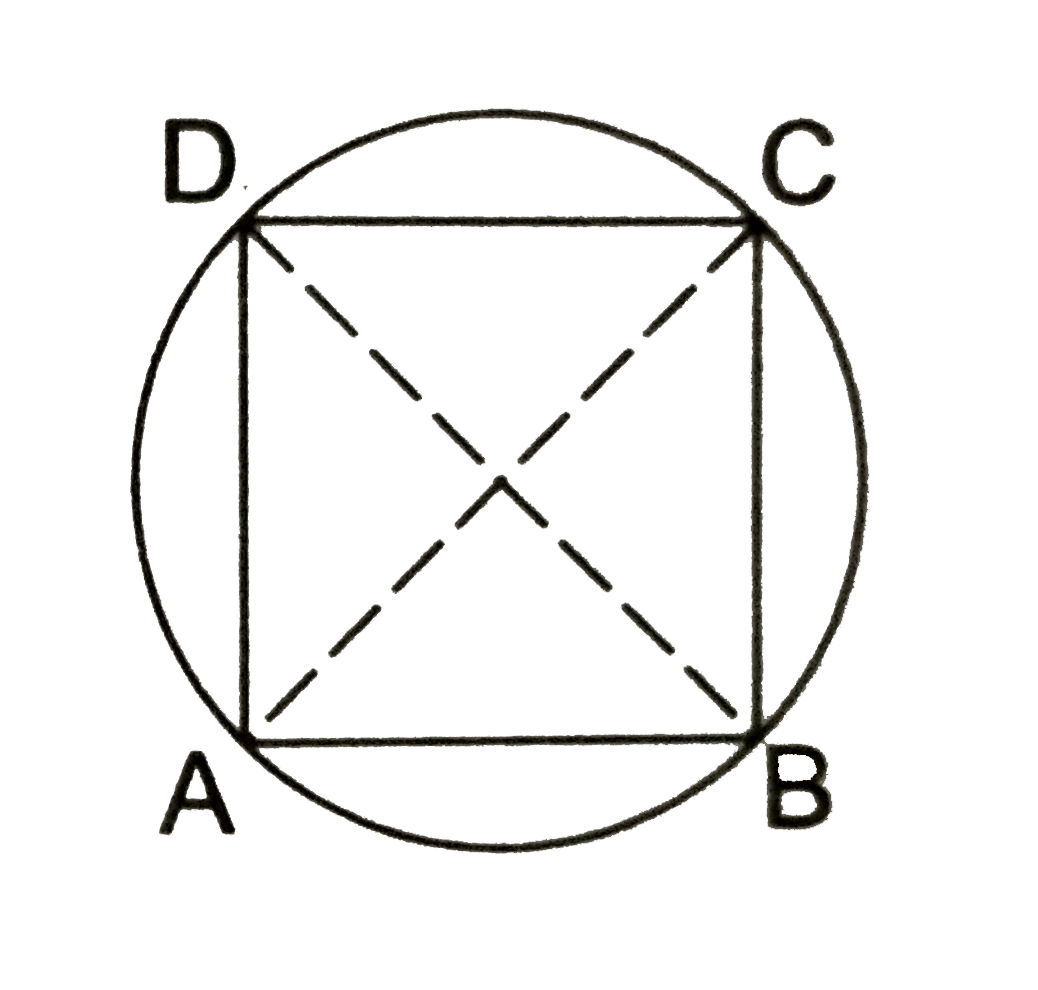
Area of the circle =(227×7×7)cm2=154cm2
Required area =(154−91)cm2=63cm2
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - Multiple Choice Questions (Mcq)26videos
AREA OF CIRCLE, SECTOR AND SEGMENT
- BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - Test Yourself19videos
AREA OF CIRCLE, SECTOR AND SEGMENT
- BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - EXERCISE1videos
AREA OF CIRCLE, SECTOR AND SEGMENT
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)30videos
ARITHMETIC PROGRESSION
Similar Questions
A square ABCD is inscribed in a circle of radius r. Find the area of the square.
View SolutionIn a circle of radius R a square is inscribed, then a circle is inscribed in the square, a new square in the circle and so on for n times. If the ratio of the limit of the sum of areas of all the circles to the limit of the sum of areas of all the squares as n→∞ is k, then find the value of 4kπ.
View Solution
Knowledge Check
- Question 1 - Select One
A square is inscribed in circle of radius R, a circle is inscribed in the square, a new square in the circle and so on for n times.
Sum of the areas of all circles isA4πR2(1−(12)n)B2πR2(1−(12)n)C3πR2(1−(13)n)DπR2(1−(12)n) - Question 2 - Select One
What is the area of the region of the circle which is situated outside the incribed square of side x ?
A(π−2)x2B(π−2)x2/2C2(π−2)x2D(π−2)x2/4 - Question 3 - Select One
ABCD is a square inscribed in a circle of radius r. Then the total area (in square units) of the portions of the circle lying outside the square is
Aπ(r2−4)B2π(r2−1)Cπ2r(r−7)Dr2(π−2)
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
View SolutionA square is inscribed in a circle of radius R, a circle is inscribed in this square then a square in this circle and so on n times. Find the limit of the sum of areas of all the squares as n→∞.
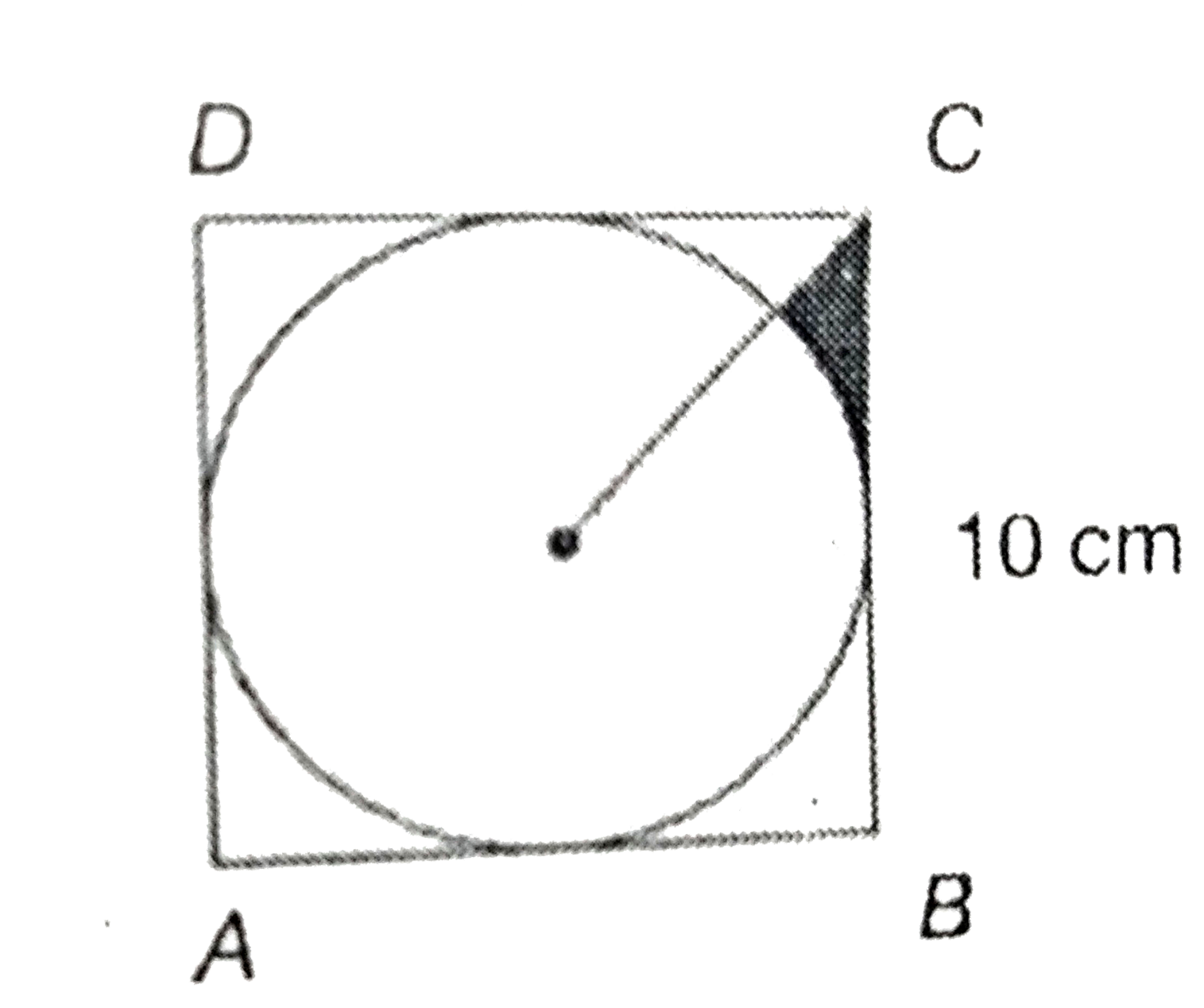
View SolutionIn the figure given below, ABCD is a square of side 10 cm and a circle is inscribed in it. Find the area of the shaded part as shown in the figure.
 View Solution
View SolutionA square of diagonal 18 cm is inscribed in a circle. Find the area included in the circle but not in the square.
View SolutionFind the area of a circle inscribed in a square of side 28 cm.
View Solution

