In the given figure, AP⊥QR,PR>PQandPQ=PS. Show that AR>AQ.

Video Solution
Text Solution
In ΔAPQandΔAPS, we have
PQ=PA (given)
∠APQ=∠APS (each equal to 90∘)
AP=AP (common)
∴ ΔAPQ≅ΔAPS (SAS-criteria).
∴ ∠AQP=∠ASP⇒∠AQS=∠ASQ. ...(i)
Now, side RS of ΔARS has been produced to Q.
∴ ∠ASQ>∠ARS [using (i)]
⇒ ∠AQR>∠ARS
⇒ AR>AQ [the side opposite to greater angle is larger].
Hence, AR gt AQ.
|
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
In the given figure, PR > PQ and PS bisects ∠ QPR. Prove that ∠PSR>∠PSQ.
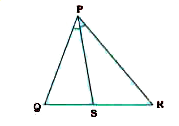
View SolutionIn the given figure, PS=PR and ∠TPS=∠QPR. Prove that PT=PQ.

View SolutionIn the given figure, PS=PR,∠TPS=∠QPR. Prove that PT=PQ.
View SolutionIn the adjoining figure, PQ=PR. Show that PS>PQ.
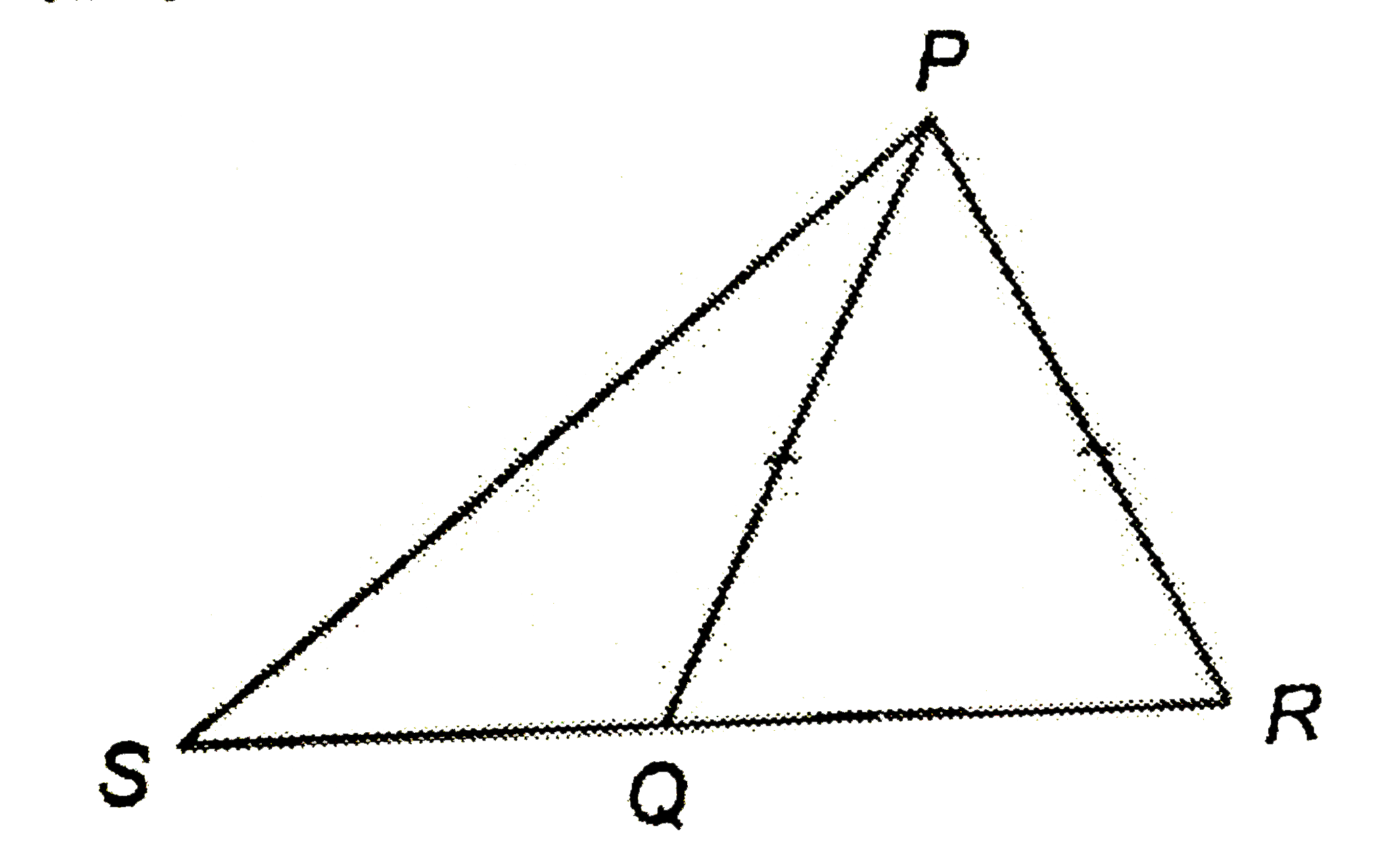
View SolutionIn Figure, PQ=PR. Show that PS>PQ
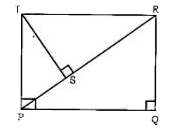
View SolutionIn the figure, RQ⊥PQ, PQ⊥PT and ST⊥PR. Prove that: ST × QR = PS × PQ
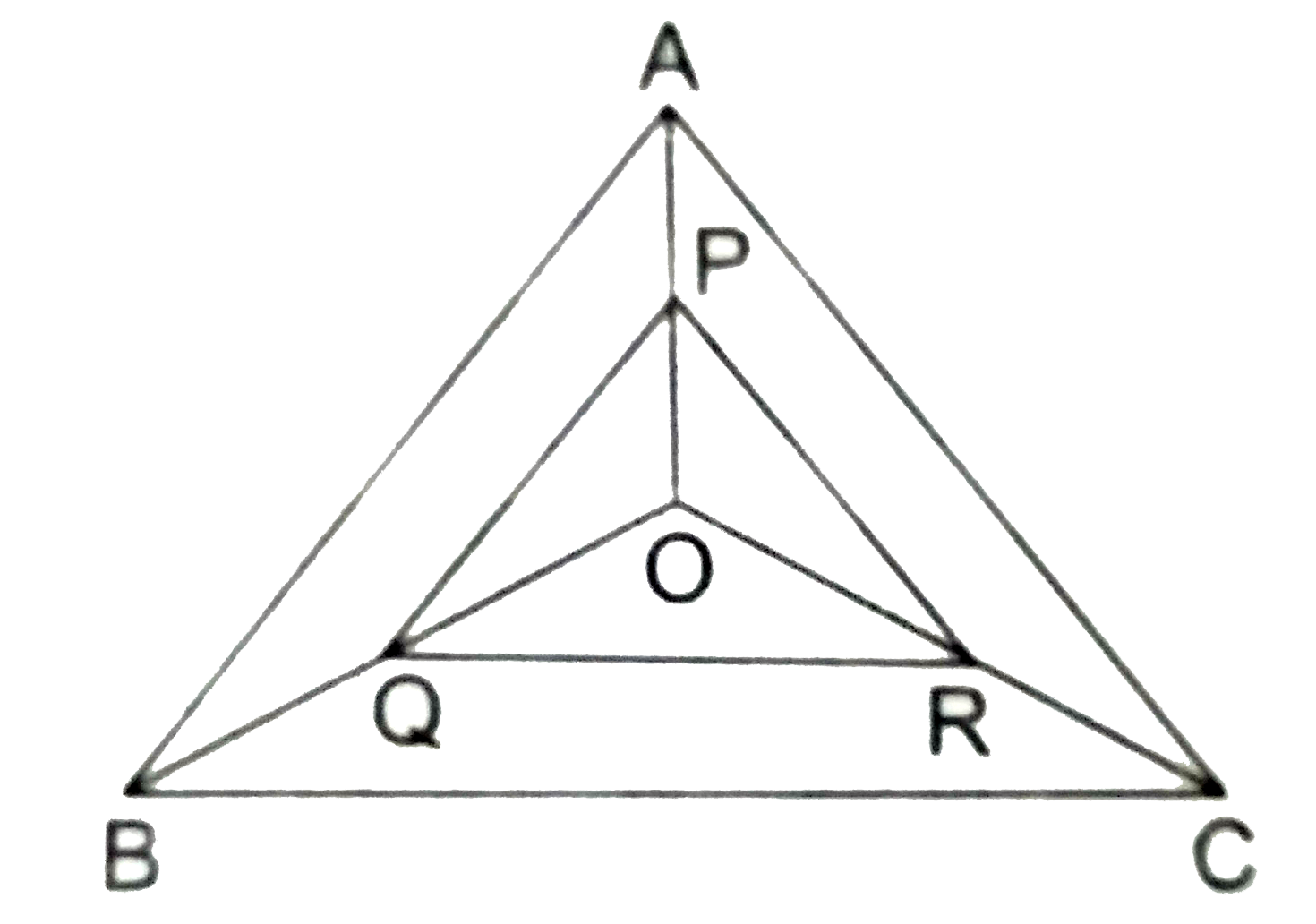
View SolutionIn the given figure, PQ||ABandPR||AC.
Prove that QR∣∣BC
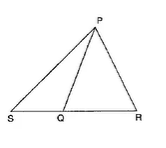
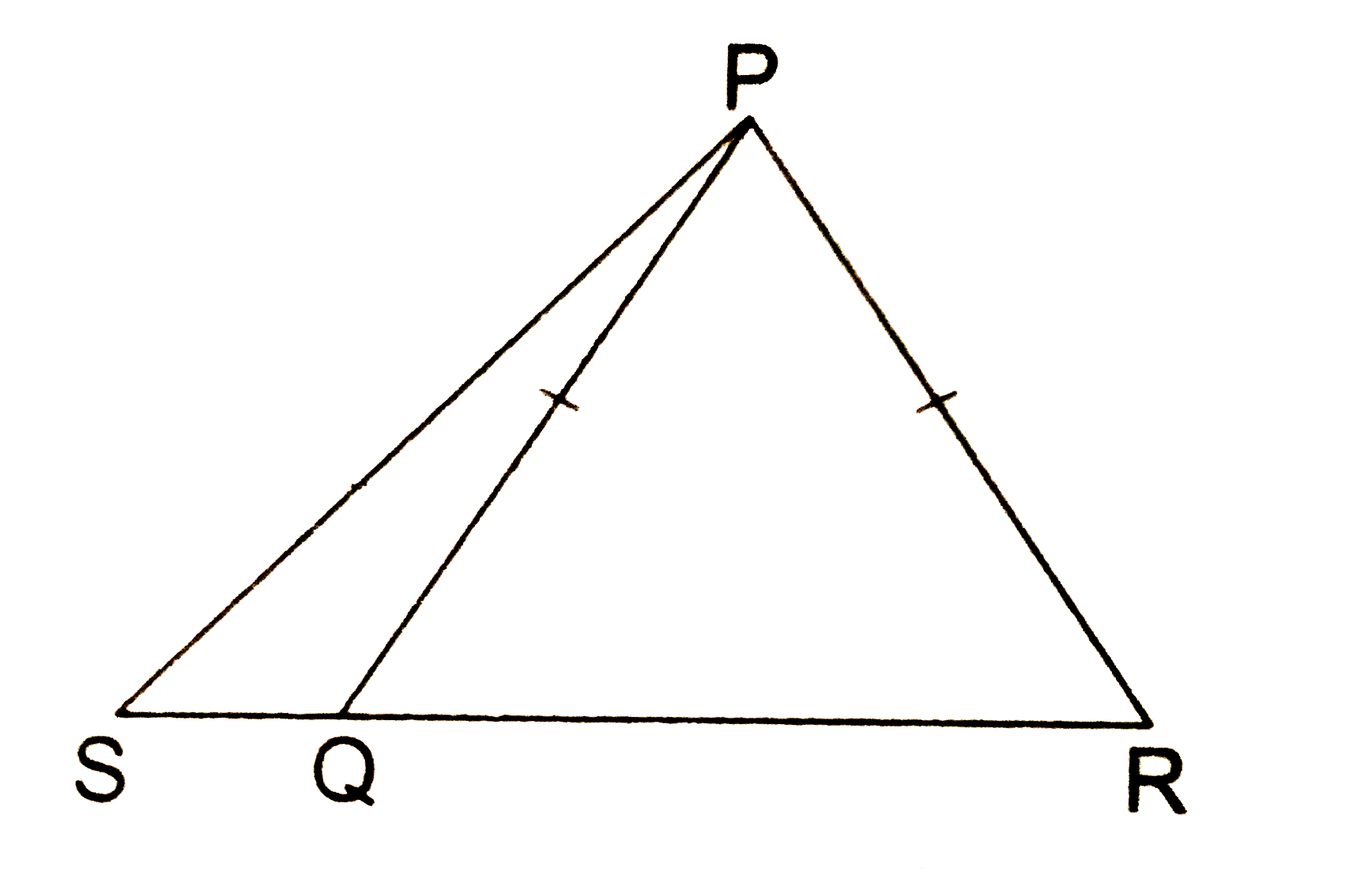
View SolutionIn the given figure, Q is a point on the side SR of ΔPSR such that PQ = PR. Prove that PS>PQ.
View SolutionIn the adjoining figure , if PQ=6,QR=10,PS=8 , find TS.
View SolutionIn the figure, if PQ=6,QR=10,PS=4 , find TS
View Solution
