In the given figure, AB>AC. If D is any point on BC, show that AB>AD.
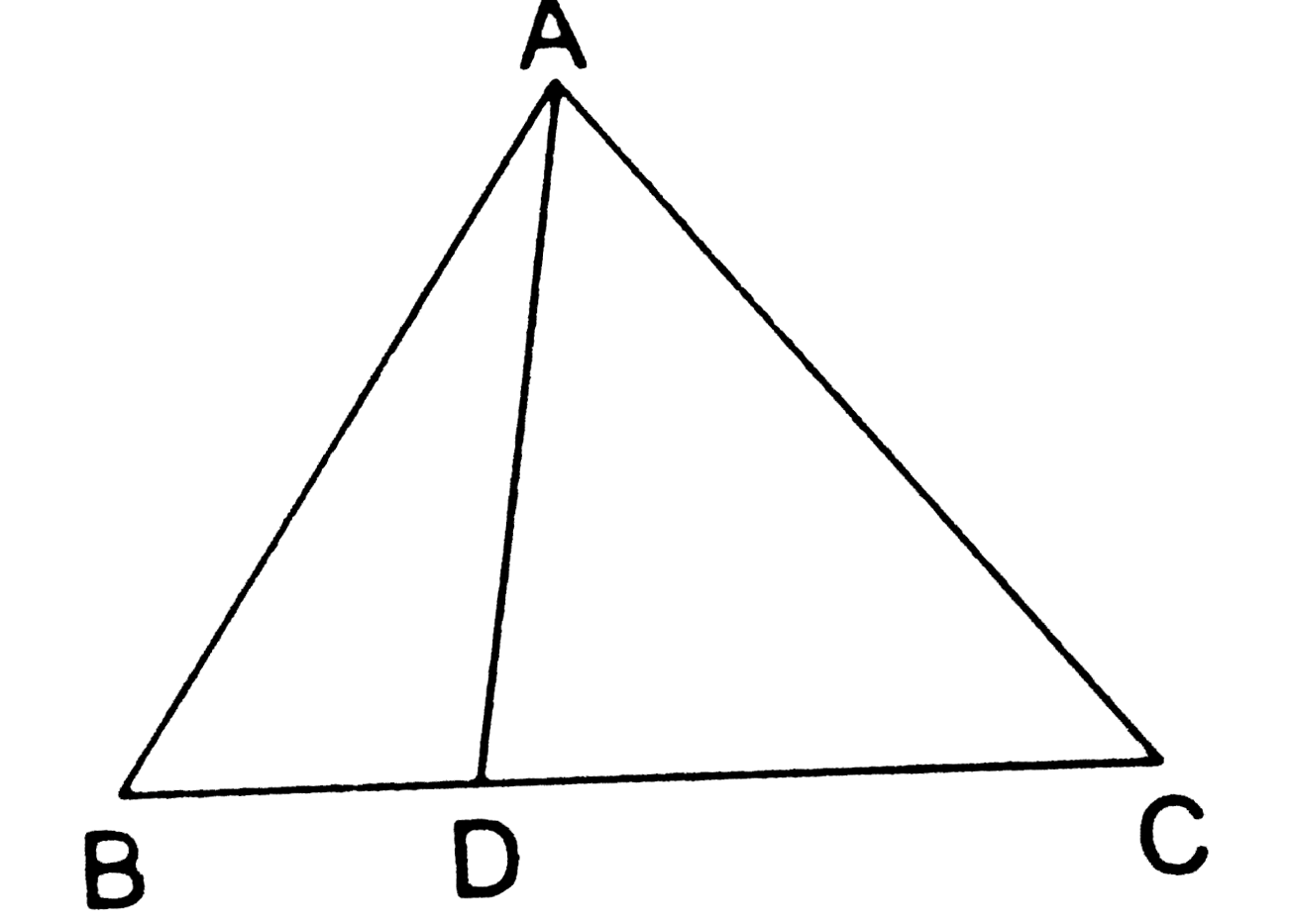
We know that the angle opposite to the larger side is larger.
∴ Ab>AC⇒∠ACB>∠ABC
⇒ ∠ACD>∠ABD. …(i)
Again, side CD of ΔACD has been produced to B.
∴ ext. ∠ADB>∠ACD. ...(ii)
From (i) and (ii), we get
∠ADB>∠ACD>∠ABD
⇒ ∠ADB>∠ABD
⇒ AB>AD [side opposite to larger angle is larger].
Hence, AB>AD.
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
In △ABC,AB>AC and D is any point on BC. Prove that, AB > AD.
View SolutionIn ΔABC, if D is any point on the side BC, show that (AB+BC+AC)>2AD.

View SolutionIn the given figure, AB||CDandO is the midpoint of AD.
Show that (i) ΔAOB≅ΔDOC.
(ii) O is the midpoint of BC.

View SolutionIn the given figure , D is a point on the side BC of ΔABC such that ∠ADC=∠BAC. Prove that CA2=CB×CD.
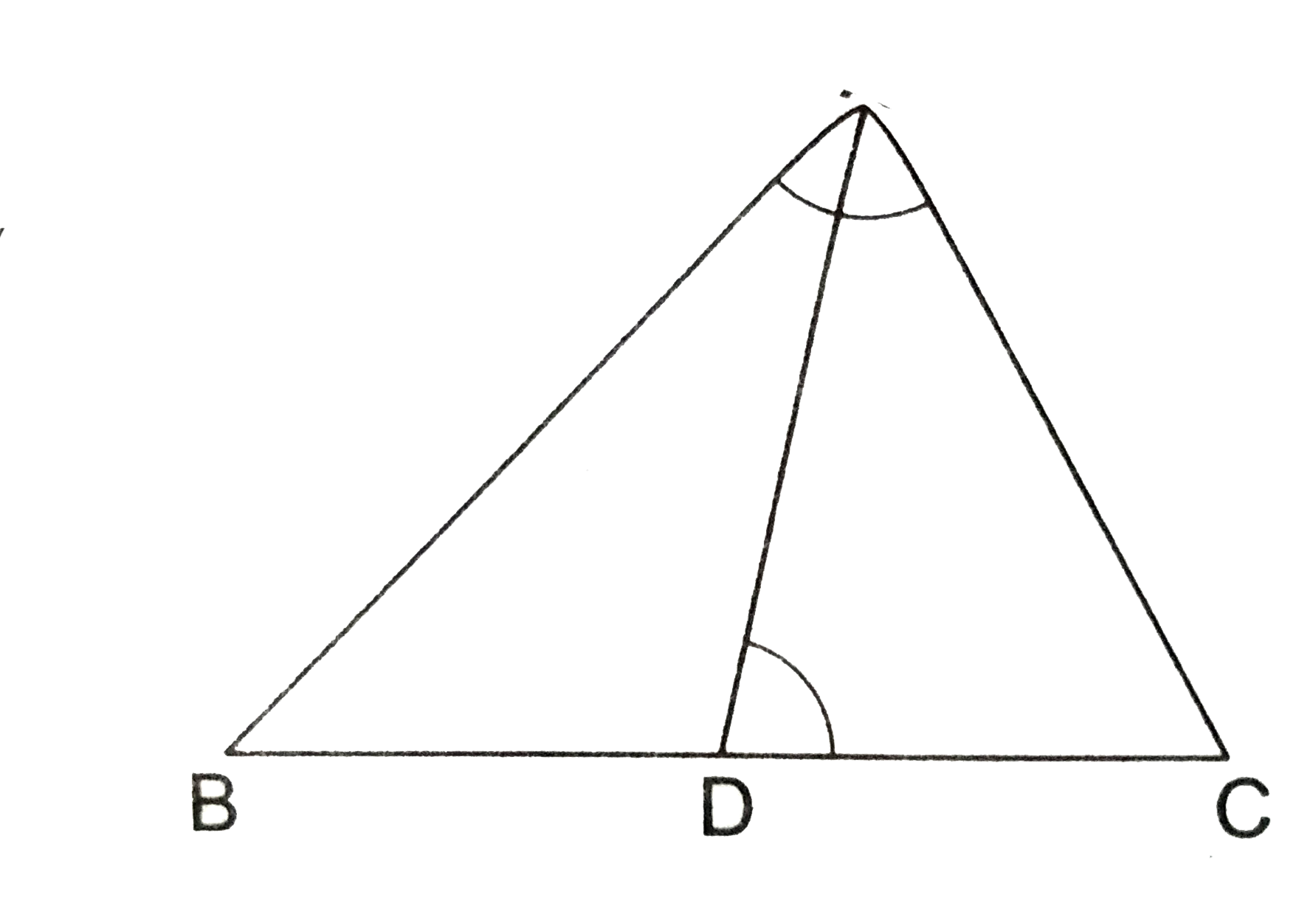
View SolutionIn the given figure, D is the mid-point of BC, E is the mid-point of BD and O is the mid-point of AE. Find the ratio of area of ΔBOEandΔABC

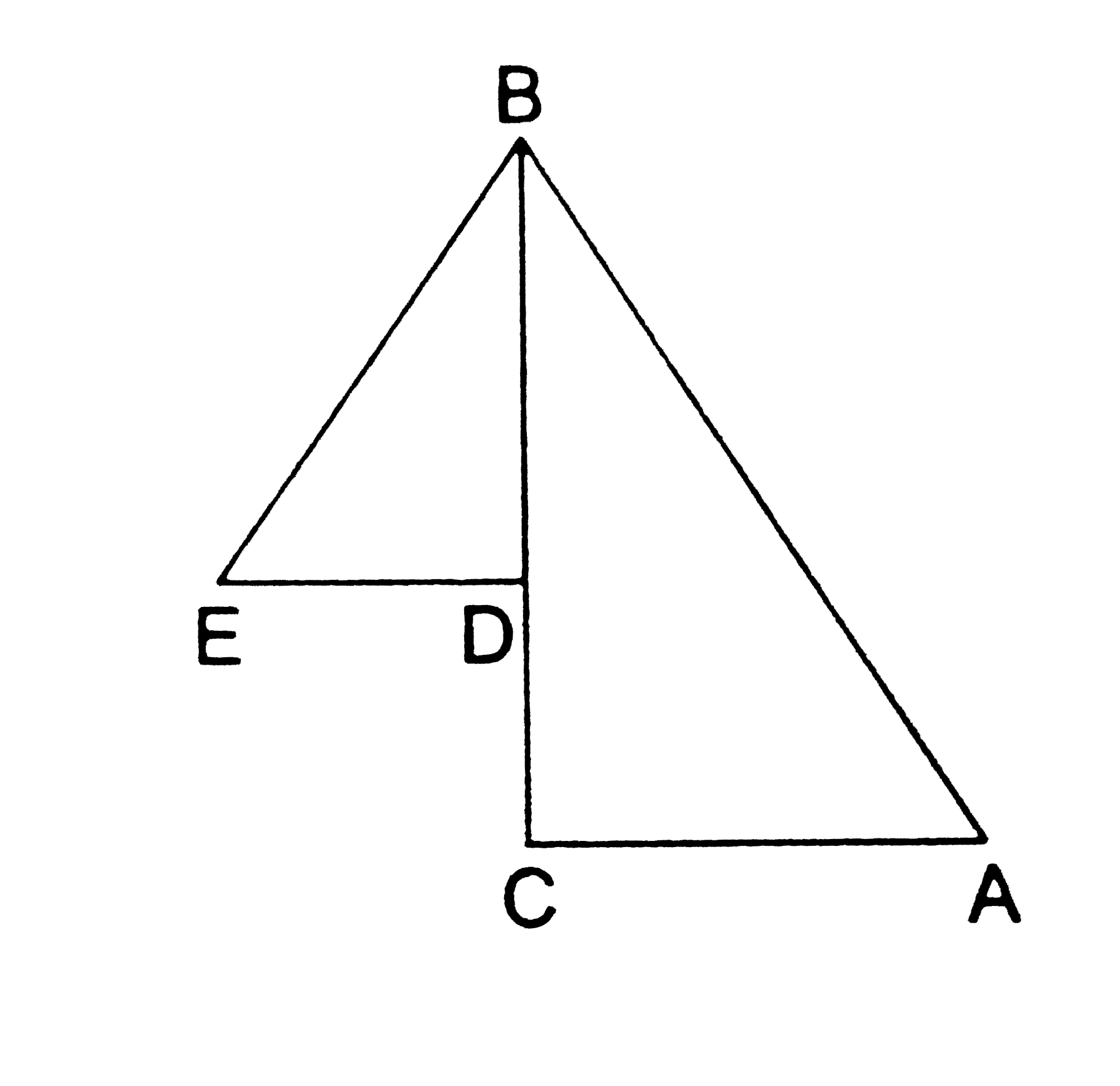
View SolutionIn the given figure, D is a point on side BC of a ΔABC and E is a point such that CD = DE.
Prove that AB+AC>BE.
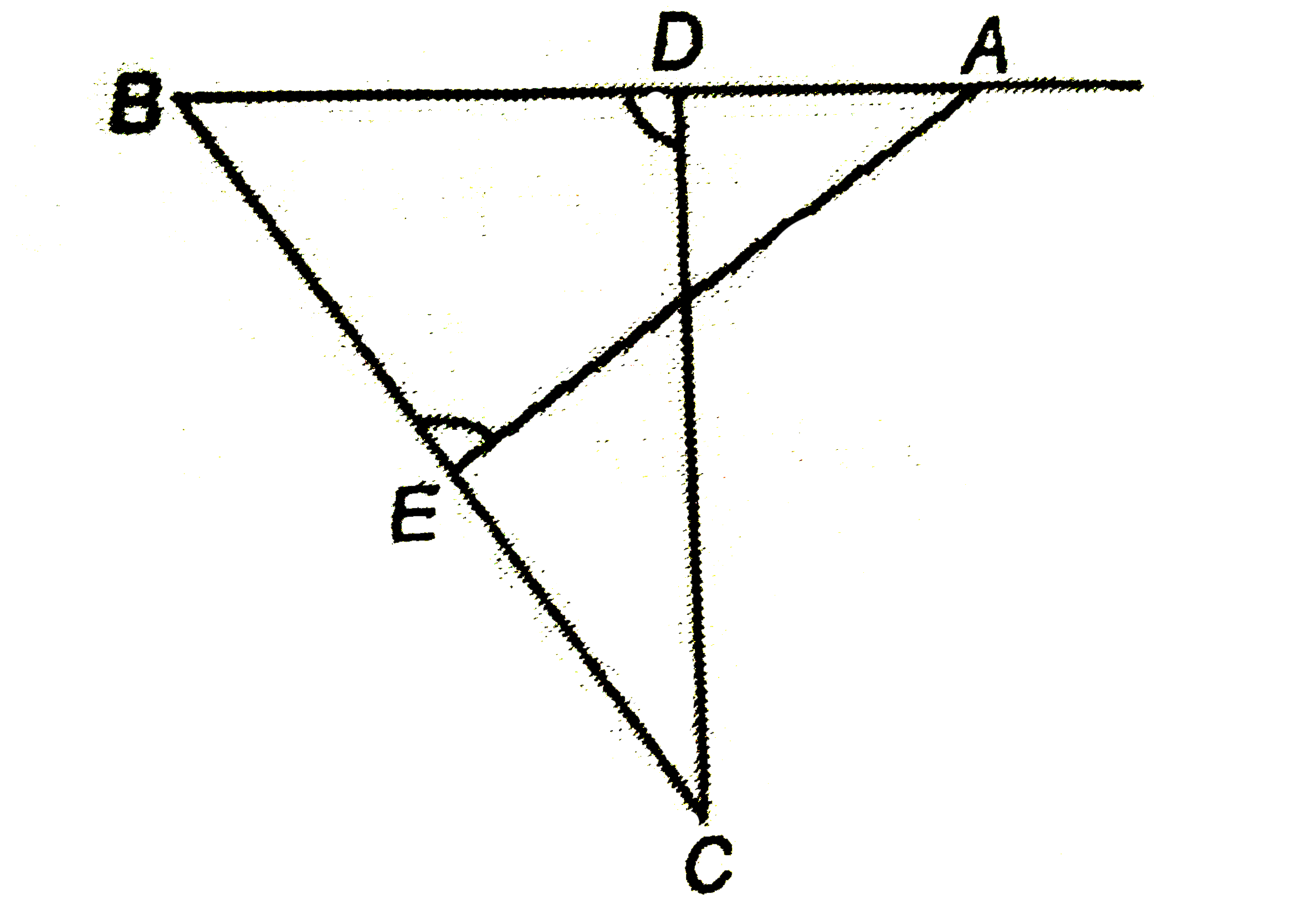
View SolutionIn the given figure, ∠BDC=∠BEA and AB=BC. Show that AE=CD.
View SolutionIn the given figure, D is the mid-point of BC, then the value of cotycotx is
View SolutionIn ΔABC,D is any point on side BC. Prove that
AB+BC+CA>2AD
View SolutionIn the given figure if DE|| BC . Then EC =
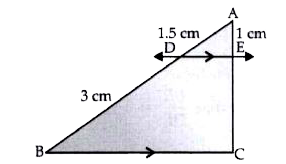
View Solution
