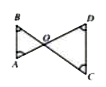
In the given figre, ∠B<∠Aand∠C<∠D. Show that AD<BC.
Video Solution
Text Solution
∠ACB=180∘−(70∘+60∘)=50∘. Let ∠BCD=∠BDC=x∘.
∠CBD=(180∘−60∘)=120∘.
∴ 120+x+x=180⇒x=30.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)20videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A27videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)37videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)22videos
COORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
In figure, ∠B<∠Aand∠C<∠D then
 AAD<BCBOD>OCCOB<OADNone of these
AAD<BCBOD>OCCOB<OADNone of these - Question 2 - Select One
In ΔABC, if ∠B<∠A then
ABC<CABBC<CACBC>AB+CADAB<CA - Question 3 - Select One
In a △ABC if 3∠A=4∠B=6∠C,calculate ∠A
A∠A=60∘B∠A=80∘C∠A=40∘DNone of these
In the given figure we have ∠1=∠3and∠2=∠4 show that ∠A=∠C
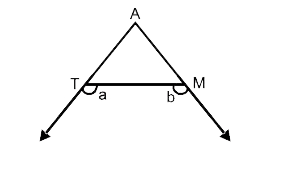
View SolutionIn the given ,figure ∠a>∠b , show that ∠ATM<∠AMT
 View Solution
View SolutionIn a triangle ABC, ∠A<∠B,∠B>∠C and ∠A=2∠C, prove that AC>BC>AB.
View SolutionIn the given figure, AD is altitude and AE is bisector of angle BAC of ΔABC. Show that ΔDAE=12(∠B−∠C)
 View Solution
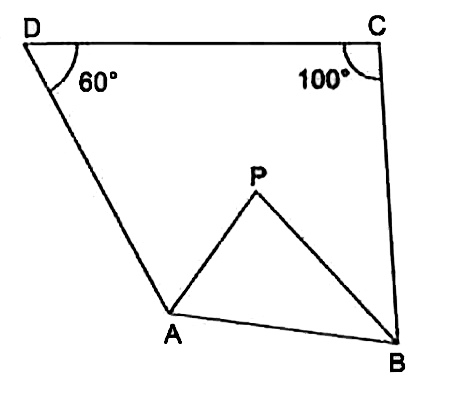
View SolutionIn the adjacent figure, the bisectors of ∠Aand∠B meet in a point P. If ∠C=100∘and∠D=60∘, find the measure of ∠APB.
 View Solution
View Solution