The variation of inductive reactance $(X_{L})$ of an inductor with the frequency (f) of the a.c. source of 100 V and variable frequency is shown in the figure.

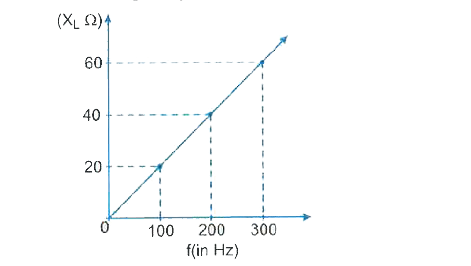
(i) Calculate the self-inductance of the inductor.
(ii) When this inductor is used in series with a capacitor of unknown value and a resistor of $10 Ω$ at 300 $s^{- 1}$ , maximum power dissipation occurs in the circuit. Calculate the capacitance of the capacitor.

Text Solution

Verified by Experts

(i) As per $X_{L}$ -f graph for a frequency f = 100 Hz , $X_{L} = 20 Ω$
$∴ X_{L} = L ω = L .2 π f$
$\Rightarrow L = \frac{X_{L}}{2 π f} = \frac{20}{2 \times 3.14 \times 100} = 0.032 H or 32$ mH
(ii) As at a frequency $f_{0} = 300 s^{- 1}$ maximum power dissipation occurs the frequecny $f_{0}$ is the resonant frequency .
We know that $f_{0} = \frac{1}{2 π \sqrt{L C}}, s o C = \frac{1}{4 π^{2} f_{0}^{2} L} \Rightarrow C = \frac{1}{4 \times {(3.14)}^{2} \times {(300)}^{2} \times 0.032} = 8.85 F$

Updated on:21/07/2023

An inductance L , a capacitor of $20 μ$ F and a resistor of $10 Ω$ are connected in series with an AC source of frequency 50 Hz . If the current is in phase with the voltage, then the inductance of the inductor is
A2.00 H
B0.51 H
C1.5 H
D0.99 H
An inductor of reactance 1 $Ω$ and a resistor of 2 $Ω$ are connected in series to the terminals of a 6 V (rms) a.c. source. The power dissipated in the circuit is
A8 W
B12 W
C14.4 W
D18 W