If the three vertices of the parallelogram ABCD are A ( 1 , a ) , B ( 3 , a ) , C ( 2 , b ) , then D is equal to

A

(3, b)

B

(6, b)

C

(0, b)

D

(5, b)

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

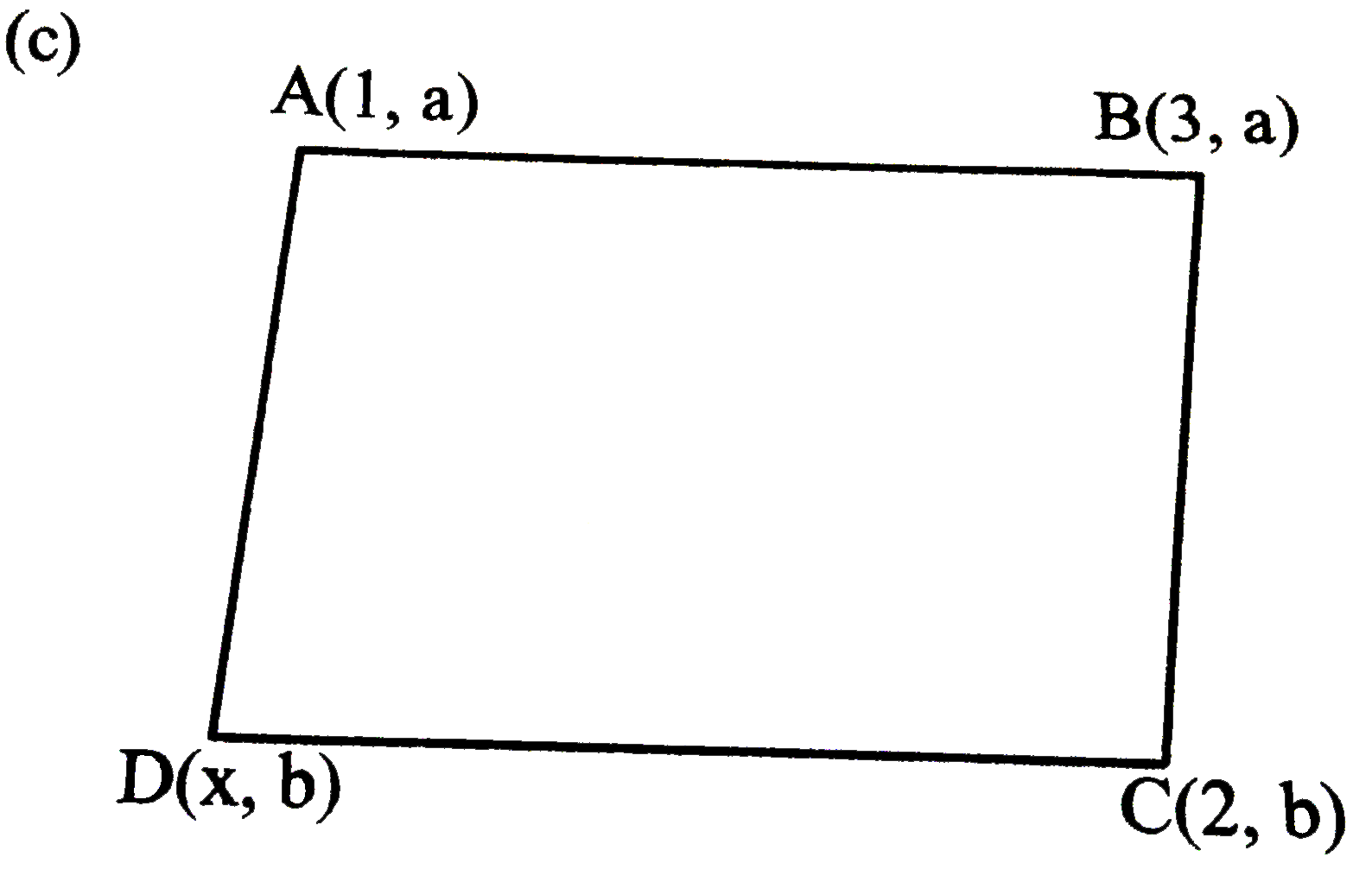
ocr_image
ABCD is a parallelogram.
A B ∣ ∣ D C , then slope of line A B = slope of line D C a - a 3 - 1
= b - y 2 - x ⇒ y = b
Also, A D ∣ ∣ B C , a - y 1 - x = a - b 3 - 2
a - b 1 - x = a - b 3 - 2 ⇒ a - b 1 - x × 1 a - b = 1
1 - x = 1
x = 0
Then points D are (0, b)

Updated on:21/07/2023
|
Class 12MATHSSTRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The vertices of a parallelogram in order are A(1, 2), B(4, y), C(x, 6), D(3, 5), then (x, y) =

    A(3 , b)
    B(0 , b)
    C(4 , b)
    D(5 , b)

  • If the three vertices of a parallelogram ABCD are
    A(3, -1, 5), B(1, -2, -4) and C(0, 3, 0), then the
    coordinates of fourth vertex is

    A(2, 4, 9)
    B(2, -4, -9)
    C(0, 4, 9)
    D(0, -4, -9)

  • The co-ordinates of three vertices of a parallelogram ABCD are A(1,0) , B(3,4) and C(1,2). The co-ordinates of fourth vertex D are :

    A(−1,2)
    B(−5,−4)
    C(1,2)
    D(2,0)