Find the area of the greatest rectangle that can be inscribed in an ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$

A

ab

B

2 ab

C

$a b / 2$

D

$\sqrt{a b}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Given equation of ellipse, $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$
Let $A (a cos θ, b sin θ)$ be any point on elllipse (1 st quadrant)
Coordinate of $B = [a cos (π - θ), b e sin (π - θ)]$ (2nd quadrant)
$= (- a cos, θ, b sin θ)$
Coordinate of $C = - [a cos (π + θ), b sin (π + θ)]$ (3rd quadrant)
Coordinate of $D = [a cos (2 π - θ), b sin (2 π - θ)]$ (4th quadrant )

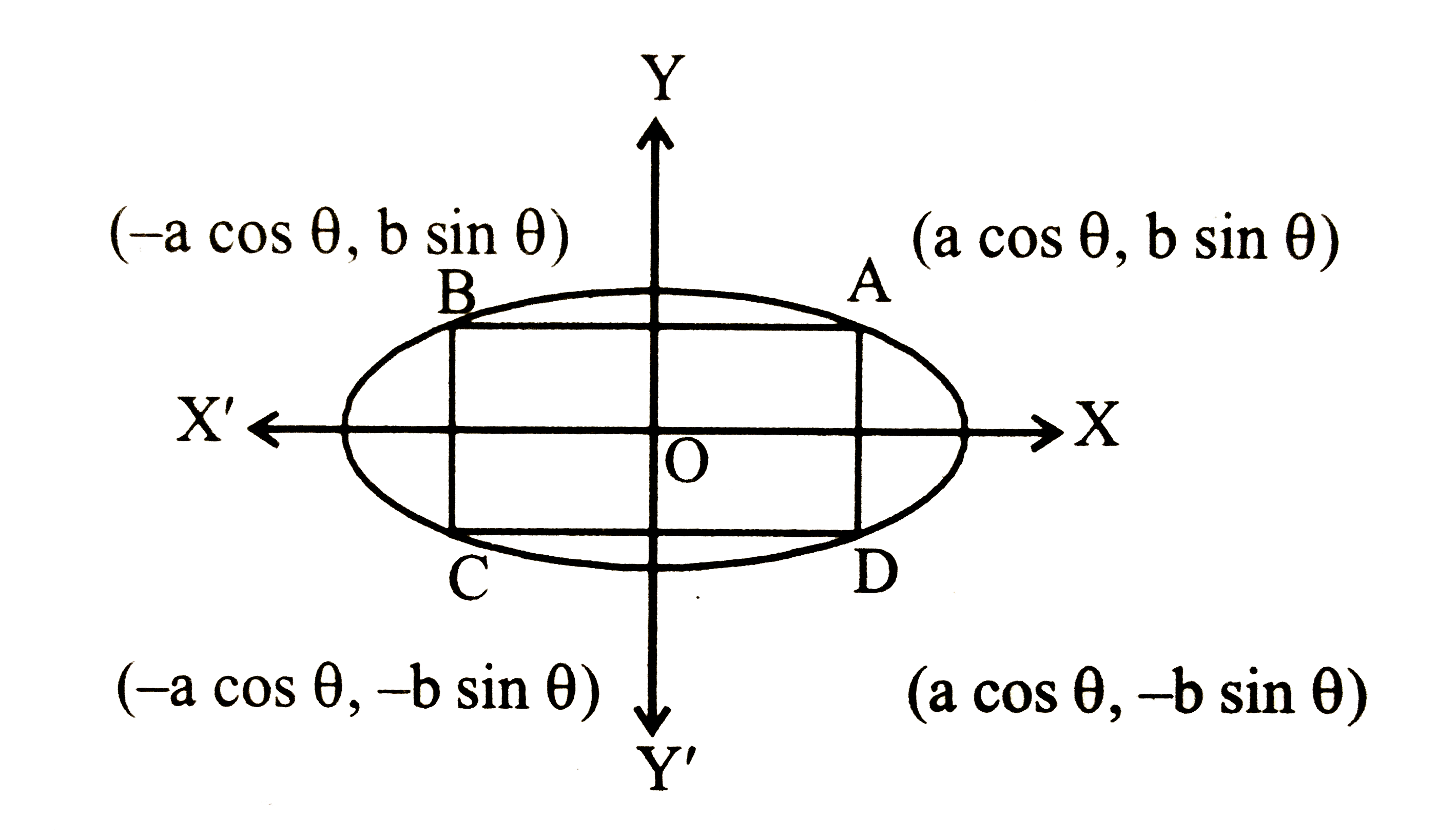
Area of the rectangle ABCD
$= (a cos θ + a cos θ) (b sin θ + b sin θ)$
$= 2 a cos θ \times 2 b sin θ = 2 a b sin 2 θ$
$= 2 a b \times 1 = 2 a b$

|

Updated on:21/07/2023

Class 12 MATHS CONICS - PARABOLA, ELLIPSE & HYPERBOLA

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Find the area of the greatest rectangle that can be inscribed in an ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$
A $\sqrt{a b}$
B $a / b$
C $2 a b$
D $a b$
Question 2 - Select One
The sides of the greatest rectangle that can be inscribed in the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ are
A $a \sqrt{2}, b \sqrt{2}$
B $\sqrt{a}, \sqrt{b}$
Ca,b
D $\frac{a}{\sqrt{2}}, \frac{b}{\sqrt{2}}$
Question 3 - Select One
Consider an ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$
What is the area of the greatest rectangle that can be inscribed in the ellipse?
Aab
B2ab
Cab/2
D $\sqrt{a b}$

NDA PREVIOUS YEARS-CONICS - PARABOLA, ELLIPSE & HYPERBOLA-MATH

Home
Ask Doubt
Profile