Find the area of the greatest rectangle that can be inscribed in an ellipse x2a2+y2b2=1
A
ab(π−1)
B
2a(π−1
C
ab(π−2)
D
None of these
Video Solution
Text Solution
The correct Answer is:C
x2a2+y2b2=1
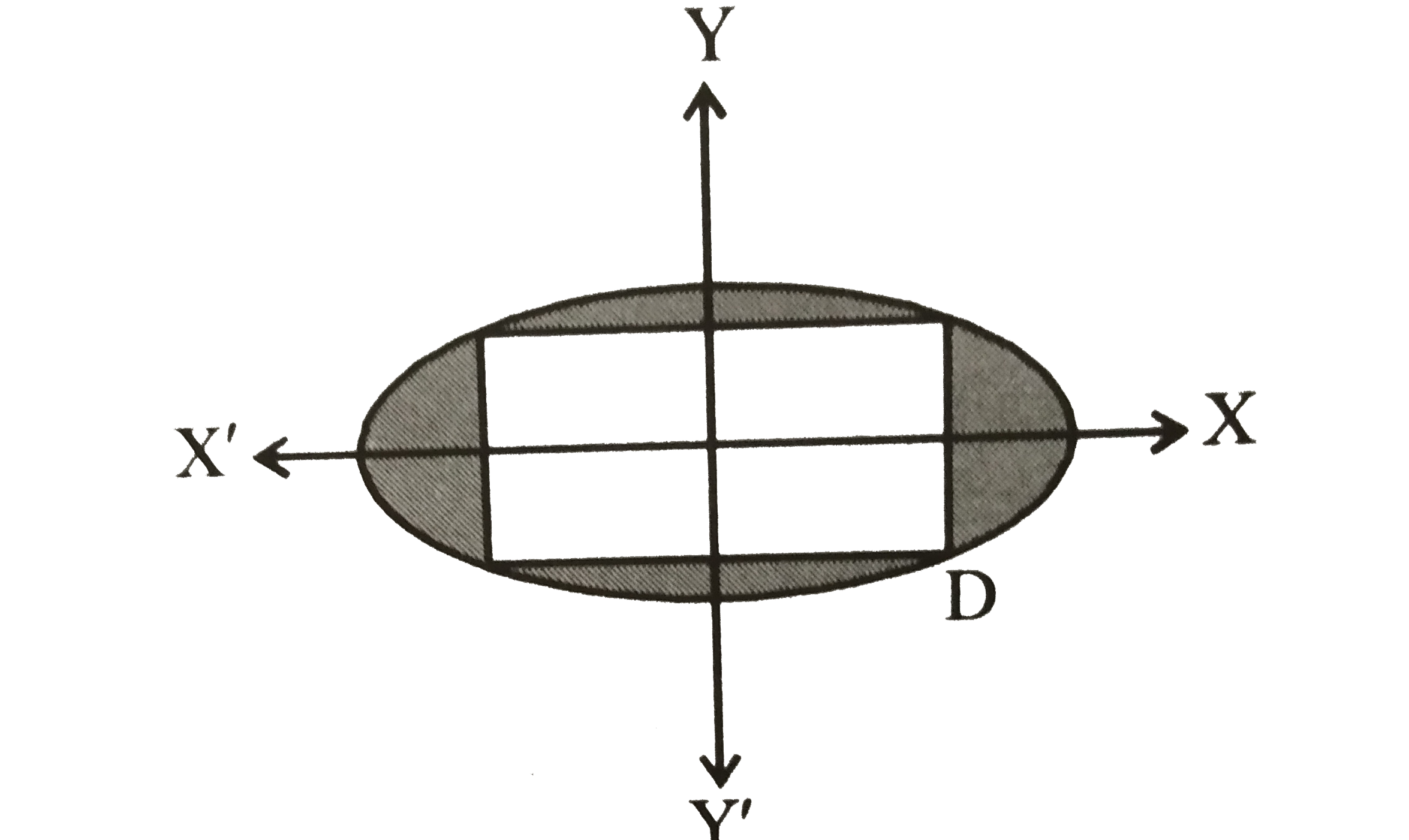
Area of ellipse is π ab
Area of shaded refion = Area of ellipse - Area of rectangle
=πab−2ab=ab(π−2)
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find the area of the greatest rectangle that can be inscribed in an ellipse x2a2+y2b2=1
A√abBa/bC2abDabConsider an ellipse x2a2+y2b2=1
What is the area of the greatest rectangle that can be inscribed in the ellipse?AabB2abCab/2D√abThe sides of the greatest rectangle that can be inscribed in the ellipse x2a2+y2b2=1 are
Aa√2,b√2B√a,√bCa,bDa√2,b√2
Find the area of the greatest isosceles triangle that can be inscribed in the ellipse (x2a2)+(y2b2)=1 having its vertex coincident with one extremity of the major axis.
View SolutionThe greatest side of the rectangle of the greatest area that can be inscribed in the ellipse x2+2y2=8,is
View SolutionThe sides of the rectangle of the greatest area, that can be inscribed in the ellipse x2+2y2=8, are given by
View SolutionFind the area of the equilateral triangle that can be inscribed in the circle :
x2+y2−4x+6y−3=0
View SolutionThe sides of the rectangle o.f greatest area which can be inscribed in the· ellipse x28+y24=1 are given by
View Solution
