In the circuit of Fig 27-57 ε=1.2kV,c=6.5μF,R1=R2=R3=0.73MΩ. With C completely uncharged switch S is suddenly closed (at t=0). At t=0, what are (a) current i1 in resistor 1, (b) current i2 in resistor 2, and (c) current i3 in resistor 3? At t=∞ (thta is after many time constants). what are (d) i1,(e)i2and(f)i3? What is the potential difference V2 across resistor 2 at (g) t=0 and (h) t=∞? Sketch V2 versus t between these two extreme times.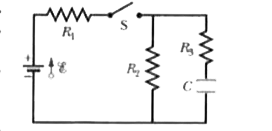 
The correct Answer is:(a) 1.1×10−3A;(b)5.5×10−4A;(c)5×10−4A(d)8.2×10−4A;(e)8.2×10−4A;(f)0;(g)4.2×102V;(h)6.0×102V (i) (##MSTAGJ∃MAPHYV02C27E02034_A01##)
Topper's Solved these Questions
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Single Correct Choice Type)
33 Videos
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (More than One Correct Choice Type)
12 Videos
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Checkpoints
7 Videos
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )
4 Videos
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - CHECK POINTS
6 Videos
Similar Questions
In the circuit shown, E=18kV,C=10μF,R1=4MΩ,R2=6MΩ,R3=3MΩ with C completely uncharged, switch S is suddenly closed (at t=0).
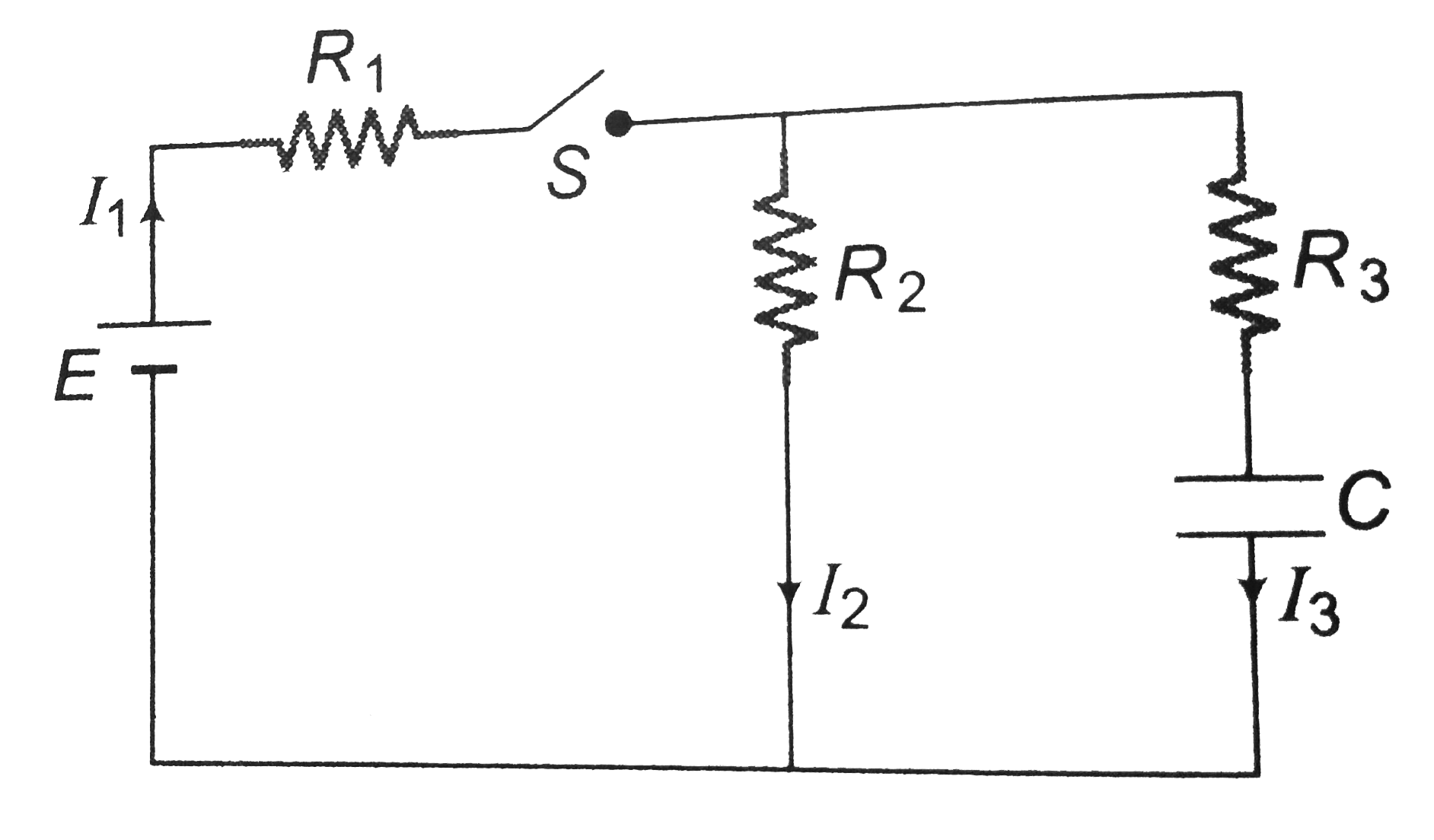
(a) Determine the current through each resistor for t=0 and t=∞
(b) What are the values of V2 (potential difference across R2) at t=0 and t=∞. ?
(c) Plot a graph of the potential differenceV2 versus t and determine the instantaneous value of V2.
View SolutionIn the circuit shown, E=18kV,C=10μF,R1=4MΩ,R2=6MΩ,R3=3MΩ with c completely uncharged, switch S is suddenly closed (at t=0).
(a) Determine the current through each resistor for t=0 and t=0
(b) What are the values of V2 (potential difference across R2) at t=0 and t=∞. ?
(c) Plot a graph of the potential differenceV2 versus t and determine the instantaneous value of V2.
View Solution
Knowledge Check
In the circuit shown below the switch is closed at t=0. For 0<t<R(C1+C2), the current I1 in the capacitor C1 in terms of total current I is
A(C1C2)IB(C2C1)IC(C1C1+C2)ID(C1(C1+C2))IIn the circuit shown, the switch is closed at t=0, the currents I1,I2 and I3 are
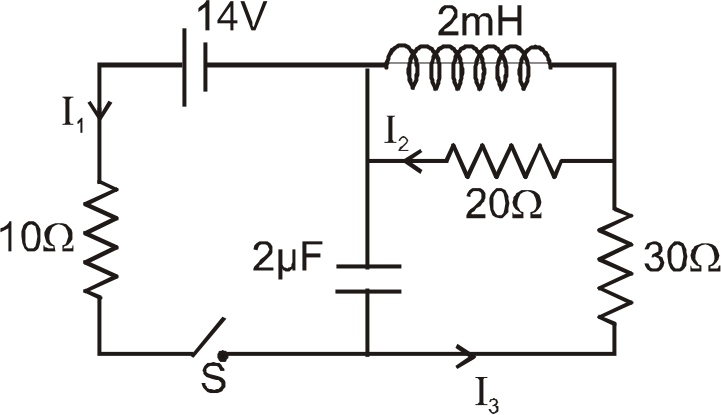A1.4A,0,0B1.4 A,0.70 A,0.70 AC0,0,0D1.2A,0.6A,0.6AThe switch S is closed in the circuit shown at time t=0 . The current in the resistor at t=0 and t=∞ are respectively .
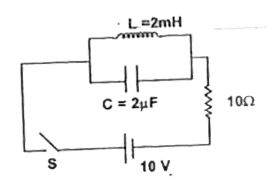A0,0 AB1,0 AC0,1 AD1,1 A
In the circuit shown below the switch is closed at t=0. For 0<t<R(C1+C2), the current I1 in the capacitor C1 in terms of total current I is
View SolutionIn the circuit shown, the switch is closed at t=0, the currents I1,I2 and I3 are
View SolutionThe switch S is closed in the circuit shown at time t=0 . The current in the resistor at t=0 and t=∞ are respectively .
View SolutionIn the circuit shows in Fig. , E=10V, R1=5Ω, R2=10Ω, and L=5H. For the two separate conditions, (i) switch S is just closed and (ii) switch S is closed for a long time, calculate
a. current i1 through R1,
b. current i2 through R2,
c. current i through the switchs,
d. the potential difference across R2,
e. the potential difference across L,
f. di2/dt.
View SolutionIn the circuit shows in Fig. , E=10V, R1=5Ω, R2=10Ω, and L=5H. For the two separate conditions, (i) switch S is just closed and (ii) switch S is closed for a long time, calculate
a. current i1 through R1,
b. current i2 through R2,
c. current i through the switchs,
d. the potential difference across R2,
e. the potential difference across L,
f. di2/dt.
View Solution