A resistance of is connected to a battery of emf 2 V and internal resistance what current is flowing through the circuit ? If another battery of double the emf is connected in series with the earlier one then current flowing in the circuit becomes double . what should be the internal resistance of battery ?
To solve the problem step by step, let's break it down into two parts: finding the current flowing through the circuit initially and then finding the required internal resistance when another battery is added.
Step 1: Calculate the initial current flowing through the circuit.
Given:
- Resistance R=1Ω
- EMF of the battery E=2V
- Internal resistance r=0.4Ω
Total resistance in the circuit:
Rtotal=R+r=1Ω+0.4Ω=1.4Ω
Using Ohm's Law to find the current I:
I=ERtotal=2V1.4Ω≈1.43A
Step 2: Analyze the situation when a second battery is added.
When another battery of double the EMF (which is 2×2V=4V) is connected in series, the total EMF becomes:
Etotal=E+E′=2V+4V=6V
According to the problem, the current doubles:
I′=2×I=2×1.43A≈2.86A
Step 3: Set up the equation to find the internal resistance of the second battery.
Using Kirchhoff's law:
Etotal=I′(R+r+r′)
Where r′ is the internal resistance of the second battery.
Substituting the known values:
6V=2.86A×(1Ω+0.4Ω+r′)
6=2.86×(1.4+r′)
Step 4: Solve for r′.
Expanding the equation:
6=2.86×1.4+2.86×r′
Calculating 2.86×1.4:
2.86×1.4≈4.004
Thus, the equation becomes:
6=4.004+2.86×r′
Rearranging gives:
2.86×r′=6−4.004
2.86×r′=1.996
Now, solving for r′:
r′=1.9962.86≈0.698Ω
Final Answer:
The internal resistance of the second battery should be approximately 0.698Ω.
---
- Resistance R=1Ω
- EMF of the battery E=2V
- Internal resistance r=0.4Ω
Rtotal=R+r=1Ω+0.4Ω=1.4Ω
I=ERtotal=2V1.4Ω≈1.43A
Etotal=E+E′=2V+4V=6V
I′=2×I=2×1.43A≈2.86A
Etotal=I′(R+r+r′)
Where r′ is the internal resistance of the second battery.
6V=2.86A×(1Ω+0.4Ω+r′)
6=2.86×(1.4+r′)
6=2.86×1.4+2.86×r′
Calculating 2.86×1.4:
2.86×1.4≈4.004
Thus, the equation becomes:
6=4.004+2.86×r′
Rearranging gives:
2.86×r′=6−4.004
2.86×r′=1.996
Now, solving for r′:
r′=1.9962.86≈0.698Ω
The internal resistance of the second battery should be approximately 0.698Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:PRACTICE PROBLEMS
Explore 71 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:CONCEPTUAL QUESTIONS
Explore 35 Videos
- ATOMS Book:MODERN PUBLICATIONChapter:ATOMS Exercise:Chapter Practice Test
Explore 16 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:MODERN PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
A bulb of resistance 5Ω is connected to a battery of emf 4.2 V and internal resistance 1Ω. Find the current through the bulb.
View SolutionA wire of resistance 4Ω is connected to a battery having an internal resistance of 1Ω For a current of 6 A to flow through the circuit what should be the emf of the battery ?
View Solution
Knowledge Check
A series combination of two resistors 1Ω each is connected to a 12 V battery of internal resistance 0.4Ω. The current flowing through it will be
A3.5AB5AC6AD10AA battery of e.m.f. 3 volt and internal resistance 1.0 ohm is connected in series with copper voltameter. The current flowing in the circuit is 1.5 amperes. The resistance of voltameter will be
AZeroB1.0ohmC1.5ohmD2.0ohmA battery of emf 2 V and initial resistance 1Ω is
connected across terminals A and B of the circuit shown
in figure
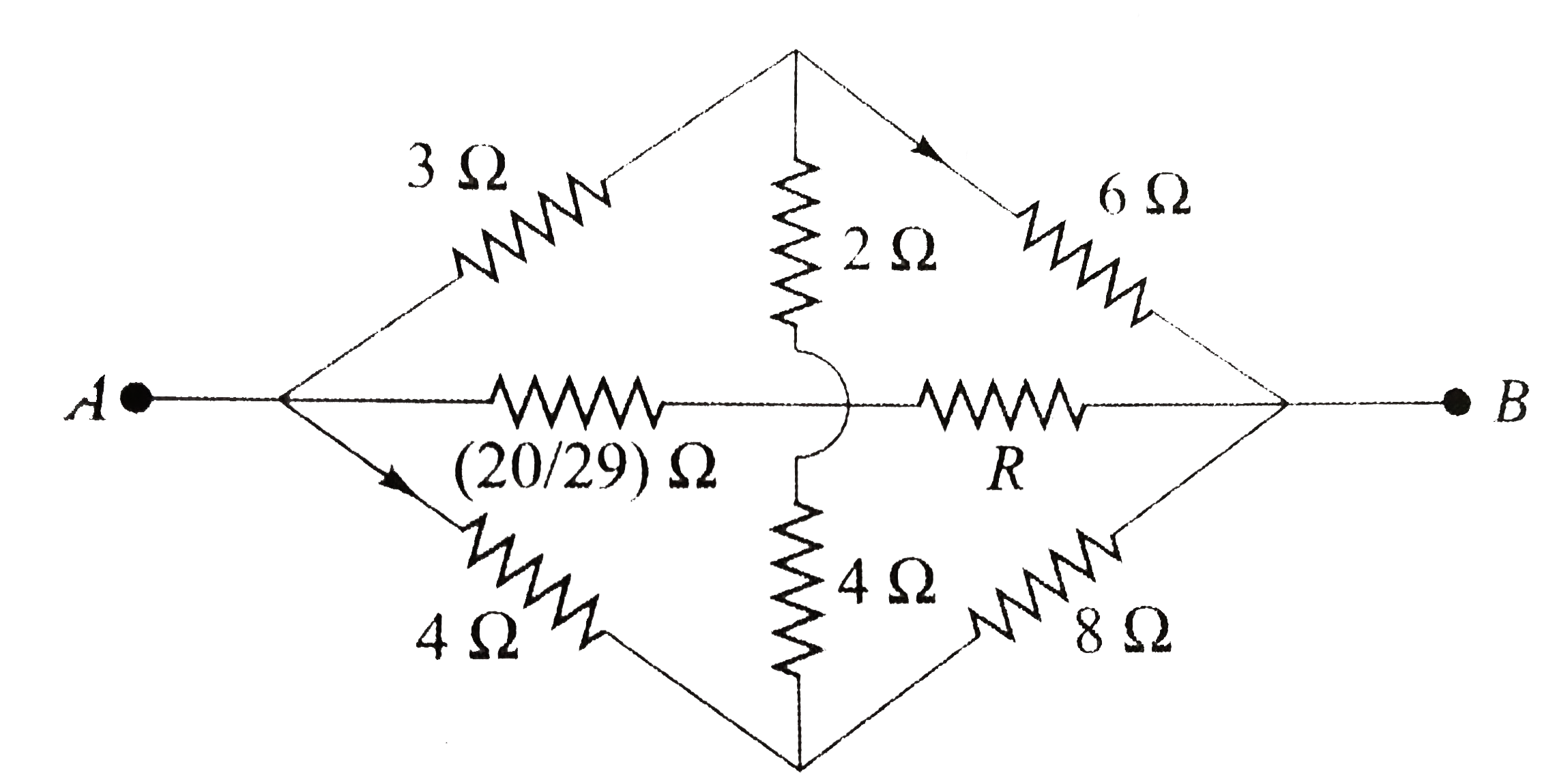 . AThermal power generated in the external circuit will be maximum possible when R=16/25Ω.BMaximum possible thermal power generated in the external circuit is equal to 4 W.CRatio of current through 3Ω to that through 8Ω is independent of R.DNone of above.
. AThermal power generated in the external circuit will be maximum possible when R=16/25Ω.BMaximum possible thermal power generated in the external circuit is equal to 4 W.CRatio of current through 3Ω to that through 8Ω is independent of R.DNone of above.
A resistor is connected to a battery of emf 10 V and internal resistance 0.3Ω. What is the resistance of the resistor to be inserted in the circuit for the circuit current 1.2A?
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance in 1 second?
View SolutionA battery of unknown emf and internal resistance is given to a student for the experiment. When student connects the battery to an external resistance of 10Ω then 1A current flows through the circuit and when the same is connected to 15Ω resistance then 0.75 A current flows through the circuit . Calculate the emf and internal resistance of the given battery.
View SolutionA battery of e.m.f 10V and internal resistance 3Omega is connected to a resistor.If the current in the circuit is 0.5A,then the resistance of the resistor is
View SolutionThree equal resistances, each of RΩ are connected as shown in figure. A battery of emf 2 V and internal resistance 0.1Ω is connected across the circuit. Calculate the value of R for which the heat generated in the circuit is maximum?
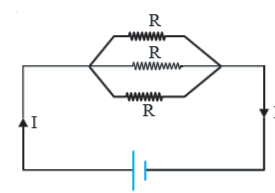
View Solution