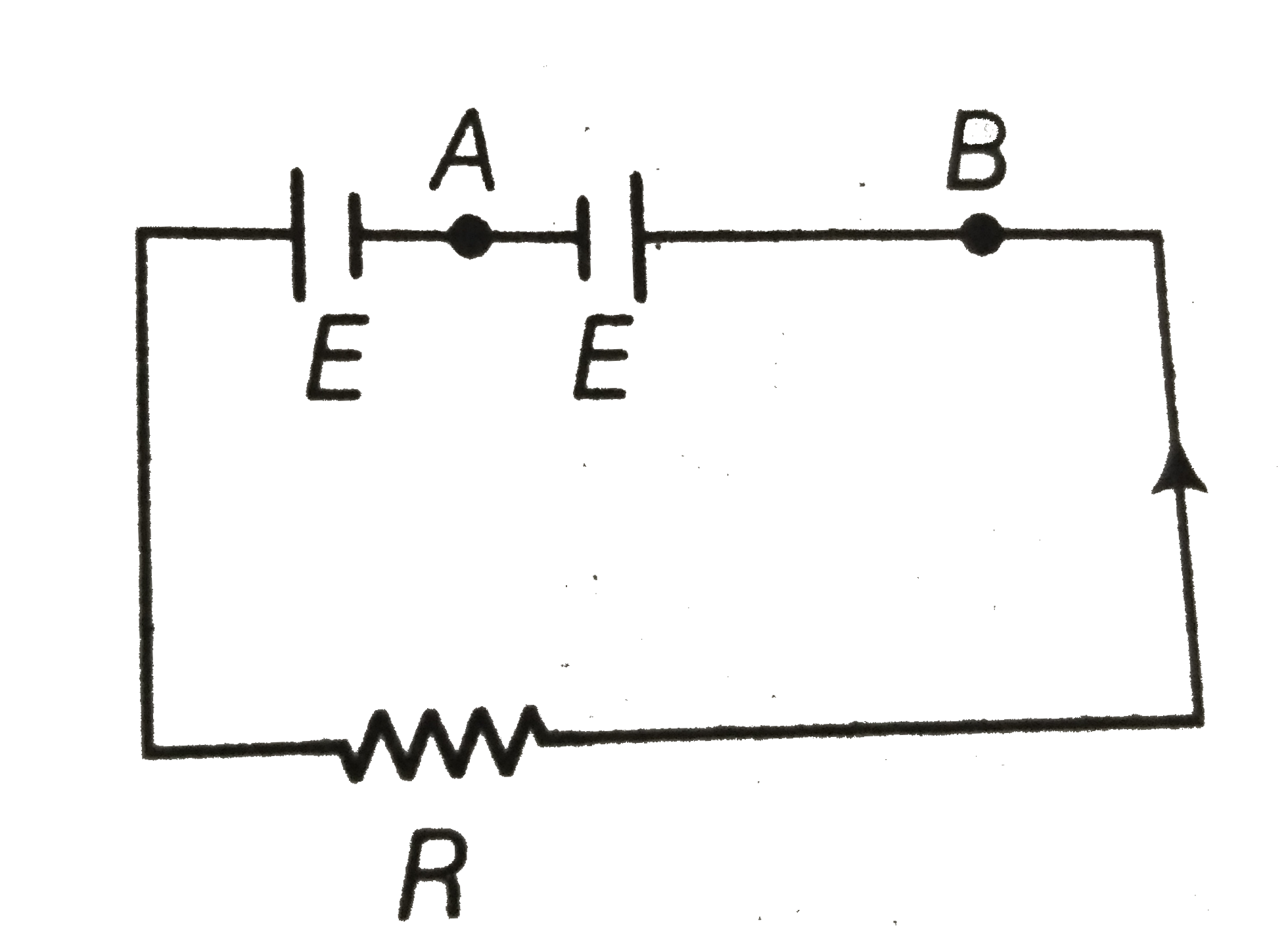
Two cells of the same emf E but internal resistance r1andr2 are connected in series to an external resistor R (Refer the figure given below). What should be the value of R so that the potential difference across the terminals of the first cell becomes zero?

Two cells of the same emf E1=E2=E are connected such as given in the figure.

Current in this network is given by
I=E+Er1+r2+R=2Er1+r2+R …(i)
We require potential drop across first cell to be zero
⇒VAB=0
⇒−E+Ir1=0
⇒E=Ir1
⇒E=2E(r1+r2+R)r1 [From (i)]
⇒R+r1+r2=2r1
∴R=(r1−r2)
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - HIGHER ORDER THINKING SKILLS & ADVANCED LEVEL
10 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - REVISION EXERCISES (VERY SHORT ANSWER QUESTIONS)
46 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT SOLVED (NCERT Exemplar Problems Subjective Questions)(Very Short Answers Type Questions)
10 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Two cells of same emf E but internal resistance r1andr2 are connected in series to an external resistor R(figure). What should be the value of R so that the potential difference across the terminals of the first cell becomes zero?
View Solution
Two cells of same emf E but internal resistance r1andr2 are connected in series to an external resistor R(figure). What should be the value of R so that the potential difference across the terminals of the first cell becomes zero?
View Solution
Knowledge Check
Tow cells with the same emf E and different internal resistances r1 and r2 are connected in series to an external resistances R . The value of R so that the potential difference across the first cell be zero is
A√r1r2Br1+r2Cr1−r2Dr1+r22Two cell with the same e.m.f. E and difference internal resistance r1andr2 are connected in series to an external resistance R a value of R be selected such that the potential difference as the flow cell E should be zero when
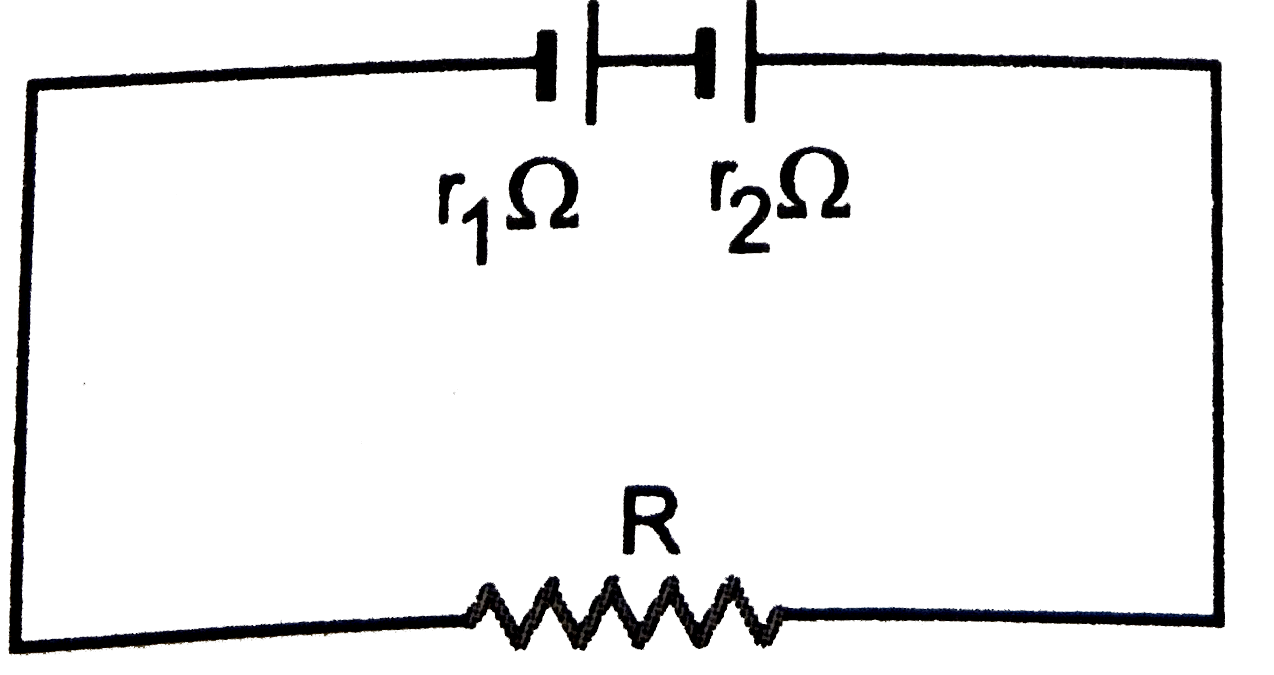 AR=r1+r2BR=r1−r2CR=r1/r2DR=r1=r2
AR=r1+r2BR=r1−r2CR=r1/r2DR=r1=r2Two cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris
 Ar1−r2Br1r2Cr1r2Dr1+r2
Ar1−r2Br1r2Cr1r2Dr1+r2
Two cells of same emf ε but internal resistances r1 and r2 are connected in series to an external resistor R. What should be the value of R so that the potential difference across the terminals of the first cell becomes zero.

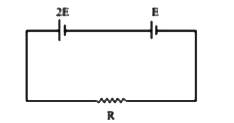
View SolutionTwo cells of emf 2E and E with internal resistance r1 and r2 respectively are connected in series to an external resistor R (see figure). The value of R, at which the potential difference across the terminals of the first cell becomes zero is
View SolutionTwo cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris

View SolutionTwo cells of emf 3V and 5V and internal resistance r1 and r2 respectively are in series with an external resistance R. if the p.d. across 1 st cell is zero, then R is
View SolutionTwo cells of same emf ε but of different internal resistances r1 and r2 are connected in series with an external resistance R. The potential drop across the first cell is found to be zero. The external resistance R is
View Solution
