Show that equivalent resistance in parallel combination is always less than each of the individual resistances connected in the combination.
To show that the equivalent resistance Req in a parallel combination is always less than each of the individual resistances connected in the combination, we can follow these steps:
Step 1: Define the equivalent resistance formula for resistors in parallel.
For two resistors R1 and R2 connected in parallel, the formula for equivalent resistance Req is given by:
1Req=1R1+1R2
Step 2: Rearrange the formula to express Req.
To find Req, we can rearrange the equation:
Req=R1R2R1+R2
Step 3: Compare Req with R1.
We want to show that Req<R1. To do this, we can set up the inequality:
R1R2R1+R2<R1
Step 4: Cross-multiply to eliminate the fraction.
Cross-multiplying gives us:
R1R2<R1(R1+R2)
Step 5: Simplify the inequality.
Expanding the right side:
R1R2<R21+R1R2
Step 6: Subtract R1R2 from both sides.
This simplifies to:
0<R21
Since R21 is always positive for any positive resistance, the inequality holds true. Thus, we have shown that:
Req<R1
Step 7: Similarly, compare Req with R2.
Following the same steps, we can show that:
Req=R1R2R1+R2<R2
By cross-multiplying and simplifying in the same manner, we will arrive at:
0<R22
This confirms that Req<R2.
Conclusion:
Thus, we have shown that the equivalent resistance Req in a parallel combination is always less than each of the individual resistances R1 and R2.
---
For two resistors R1 and R2 connected in parallel, the formula for equivalent resistance Req is given by:
To find Req, we can rearrange the equation:
We want to show that Req<R1. To do this, we can set up the inequality:
Cross-multiplying gives us:
Expanding the right side:
This simplifies to:
Following the same steps, we can show that:
Thus, we have shown that the equivalent resistance Req in a parallel combination is always less than each of the individual resistances R1 and R2.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - REVISION EXERCISES (ADDITIONAL QUESTIONS)
11 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - REVISION EXERCISES (FILL IN THE BLANKS)
10 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - HIGHER ORDER THINKING SKILLS & ADVANCED LEVEL
10 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Knowledge Check
The equivalent resistance in series combination is
Asmaller than the largest resistanceBlarger than the largest resistanceCsmaller than the smallest resistanceDlarger than the smallest resistanceThe equivalent resistance of the combination across AB is .
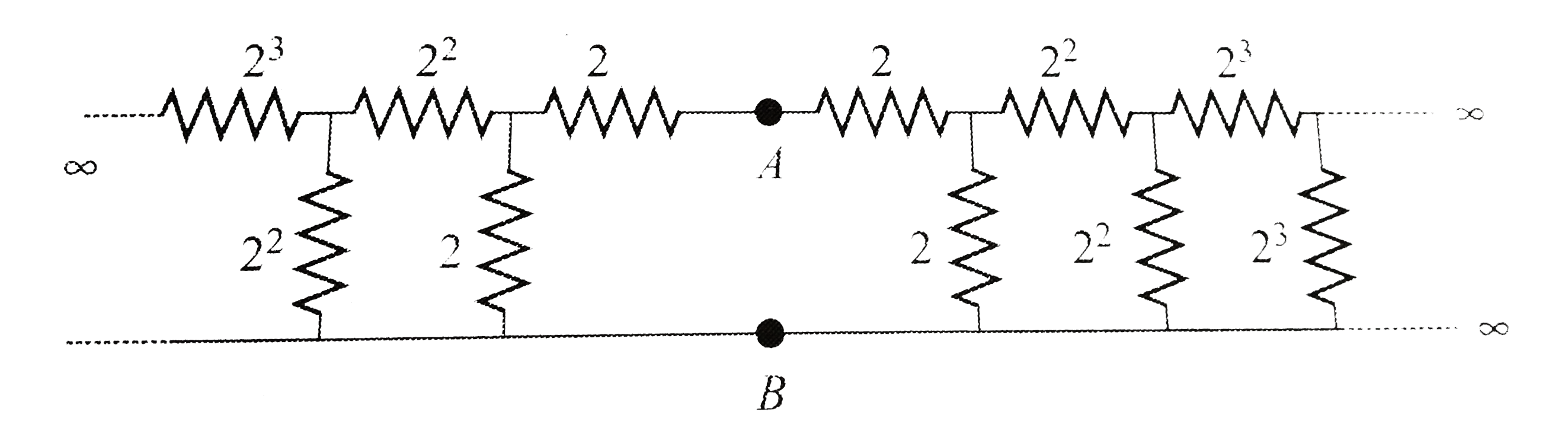 A(3+√174)B3+√17C3+√172D2(3+√17)
A(3+√174)B3+√17C3+√172D2(3+√17)The equivalent resistance of resistors connected in series is always
AEqual to the mean of component resistorsBLess than the lowest of component resistorsCIn between the lowest and the highest of component resistorsDEqual to sum of component resistors
Derive expression for equivalent resistance of a parallel combination of resistances.
(b) Calculate the ratio of equivalent resistance for a series combination of n number of identical resistors to the parallel combination of the same type of n number of resistors.
View Solution(a) what is meant by series and parallel combination of resistances ?
(b) in which case, series combination or parallel combination, the combined resistance is less than any of the individual resistances ?
(c ) How should two resistance of 2Ω each be connected so as to produce an equivalent resistance of 1Ω ?
In the circuit diagram given here , find:
(i) total resistance of the circuit
(ii) total current flowing in the circuit, and
(iii) the potential difference across R1
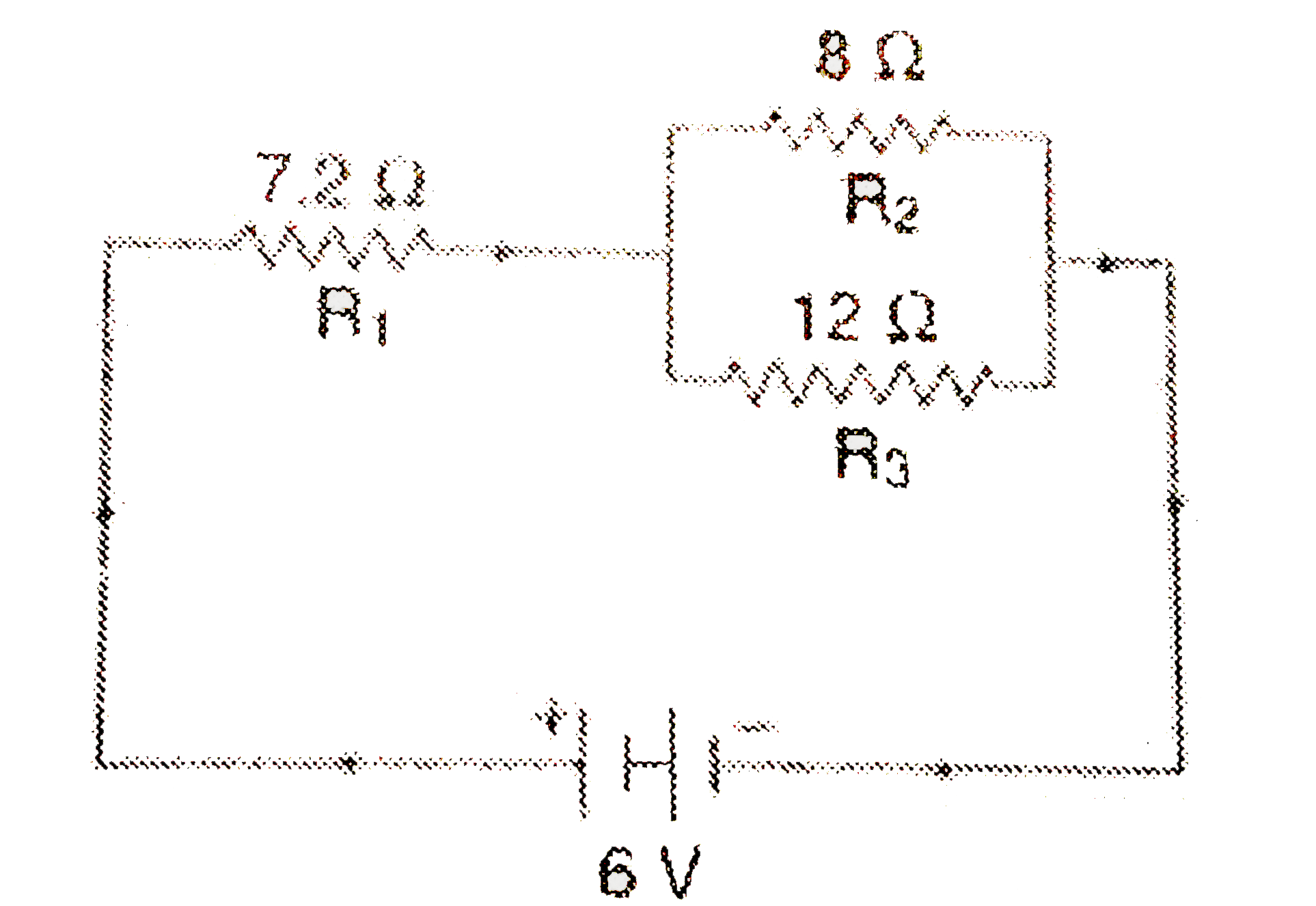
View SolutionThe equivalent resistance between point A and B for the combination of resistance

View SolutionEquivalent resistance R, of the parallel combination when two resistors Rand R, are connected in parallel is equal to
View SolutionIf 'n' number of identical resistors are connected oin parallel combination, then the effective resistance of thec combination is ______.
View Solution
