EMF of an electrical cell is 2 volt. A 10Ω resistance is joined at its two ends then potential difference is measured 1.6 volt. Find out the internal resistance and lost volt.
To solve the problem, we need to find the internal resistance of the cell and the lost voltage when a resistance of 10Ω is connected across it.
1. Identify Given Values:
- EMF of the cell (E) = 2 volts
- Resistance (R) = 10 ohms
- Measured potential difference (V) = 1.6 volts
2. Understand the Relationship:
The relationship between EMF, potential difference, internal resistance (r), and current (I) can be expressed using the formula:
V=E−I⋅r
where V is the potential difference across the external resistor.
3. Calculate the Current (I):
The current can be calculated using Ohm's law. The total resistance in the circuit is the sum of the external resistance and the internal resistance:
I=ER+r
Rearranging gives:
I=210+r
4. Substituting Current into the Voltage Equation:
Substitute I into the voltage equation:
1.6=2−(210+r)⋅r
5. Rearranging the Equation:
Rearranging the equation gives:
1.6(10+r)=2(10+r)−2r
Expanding both sides:
16+1.6r=20+2r−2r
Simplifying:
16+1.6r=20
6. Solving for Internal Resistance (r):
Rearranging gives:
1.6r=20−16
1.6r=4
Dividing both sides by 1.6:
r=41.6=2.5Ω
7. Calculate the Lost Voltage:
The lost voltage can be calculated as:
Lost Voltage=E−V=2−1.6=0.4volts
Final Answers:
- Internal Resistance (r) = 2.5Ω
- Lost Voltage = 0.4volts
- EMF of the cell (E) = 2 volts
- Resistance (R) = 10 ohms
- Measured potential difference (V) = 1.6 volts
The relationship between EMF, potential difference, internal resistance (r), and current (I) can be expressed using the formula:
V=E−I⋅r
where V is the potential difference across the external resistor.
The current can be calculated using Ohm's law. The total resistance in the circuit is the sum of the external resistance and the internal resistance:
I=ER+r
Rearranging gives:
I=210+r
Substitute I into the voltage equation:
1.6=2−(210+r)⋅r
Rearranging the equation gives:
1.6(10+r)=2(10+r)−2r
Expanding both sides:
16+1.6r=20+2r−2r
Simplifying:
16+1.6r=20
Rearranging gives:
1.6r=20−16
1.6r=4
Dividing both sides by 1.6:
r=41.6=2.5Ω
The lost voltage can be calculated as:
Lost Voltage=E−V=2−1.6=0.4volts
- Internal Resistance (r) = 2.5Ω
- Lost Voltage = 0.4volts
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - REVISION EXERCISES (ADDITIONAL QUESTIONS)
11 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - REVISION EXERCISES (FILL IN THE BLANKS)
10 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - HIGHER ORDER THINKING SKILLS & ADVANCED LEVEL
10 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
The e.m.f. of a cell is 6 volt. When 2 ampere current is drawn from it then th e potential difference across its terminal remains 3 volt. Its internal resistance.
View SolutionIn the electrical network shown in the figure, What will be the potential difference (in volt) across 3Ω resistance ?
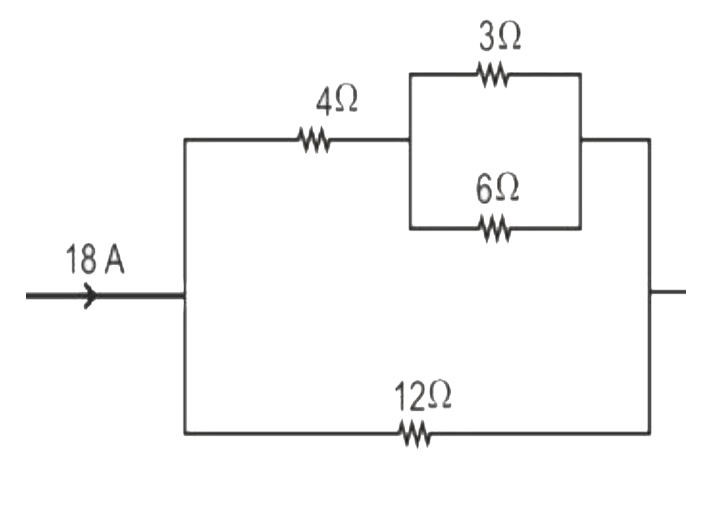
View Solution
Knowledge Check
The potential difference in open circuit for a cell is 2.2 volts. When a 4 ohm resistor is connected between its two electrodes the potential difference becomes 2 volts. The internal resistance of the cell will be
A1ohmB0.2 ohmC2.5 ohmD0.4 ohmThe potential difference in open circuit for a cell is 2.2 votls . When a 4ohmresistor is connected between its two electrodes that potential difference becomes 2 volts. The internal resistance of cell will be
A1ohmB0.2ohmC2.5ohmD0.4ohmWhen the resistance of 9Ω is connected at the ends of a battery, its potential difference decreases from 40 volt to 30 volt . The internal resistance of the battery is
A6ΩB3ΩC9ΩD15Ω
A current of 5 amperes flows through a wire whose ends are at a potential difference of 3 volts. Calculate the resistance of the wire.
View SolutionA cell of emf 1.5 V is connected with an external resistance 20Ω. The potential difference falls to 1.0 V. The internal resistance of cell is
View SolutionA cell of emf 1.5 Vis connected with an external resistance 2Ω. The potential difference falls to 1.0 v. The internal resistance of cell is
View SolutionA cell of emf 1.5 Vis connected with an external resistance 2Ω. The potential difference falls to 1.0 v. The internal resistance of cell is
View SolutionTwo resistance of 400Ω and 800Ω are connected in series with 6 volt battery of negligible internal resistance. A voltmeter of resistance 10,000Ω is used to measure the potential difference across 400Ω. The error in measurement of potential difference in volts approximatley is
View Solution
