A uniform wire of resistance 12Ω is cut into three pieces so that the ratio of the resistances R1:R2:R3=1:2:3 and the three pieces are connected to form a triangle across which a cell of emf 8 V and internal resistance 1Ω is connected as shown.
Calculate the current through each part of the circuit.

R1+R2+R3=12Ω
(1+2+3)x=12Ω
⇒x=2Ω
Net resistance of the combination of resistances,
RAC=R.R3R3+R.
RAC=3612=3Ω
Current in this network
I=ERAC+r=83+1=2A
Voltage across the branch R3=E−Ir
=8=2×1=6V,=I.R3
Current in branch R3⇒I.=6R3=66=1A
Current in branch R1andR2=I−I.=2−1=1A
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (A. MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER)
36 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION FOR COMPETITIVE EXAMINATIONS)
20 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - REVISION EXERCISES (LONG ANSWER QUESTIONS)
10 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A uniform wire of resistance 12Ω is cut into three pieces in the ratio 1 : 2 : 3 and the three pieces are connected to form a triangle. A cell of emf 8 V and internal resistance 1Ω is connected across the highest of the three resistors. Calculate the current through each part of the circuit.
View Solution
The diagram above shows three resistors connected across a cell of e.m.f. 1.8 V and internal resistance r. Calculate :
Current through 3Ω resistor.
View Solution
Knowledge Check
A cell of emf 2 V and internal resistance 0.1Ω is connected with a resistance of 3.9Ω The voltage across the cell terminal will be
A1.95VB1.90VC0.50VD2.00VThree equal resistances, each of RΩ are connected as shown in figure. A battery of emf 2 V and internal resistance 0.1Ω is connected across the circuit. Calculate the value of R for which the heat generated in the circuit is maximum?
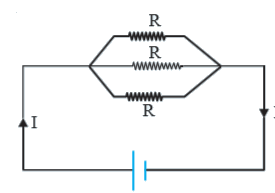 A0.2ΩB0.3ΩC0.4ΩDnone of these
A0.2ΩB0.3ΩC0.4ΩDnone of theseA cell of emf 2.0 V and internal resistance 0.1 Ω is connected with a resistance of 3.9Ω. The voltage across the cell terminals will be
A0.50 VB1.90 VC1.95 VD2.0 V
A wire of uniform cross section of resistance 16Ω is divided into four pieces in the ratio of 1 : 2 : 3 : 4 and ll the four resistros are connected in the form of a square . Calculate the current drawn from the battery, if a battery of emf 10 V and internal resistance 0.5Ω is connected across the resistor with least resistance.
View SolutionThree equal resistances, each of RΩ are connected as shown in figure. A battery of emf 2 V and internal resistance 0.1Ω is connected across the circuit. Calculate the value of R for which the heat generated in the circuit is maximum?

View SolutionThree equal resistace, each of R ohm, are connectedd as shown in the figure. A battery of 2V and of internal resistance 0.1 ohm is connected across the circuit. The value of R for which the heat generated in the circuit maximum will be
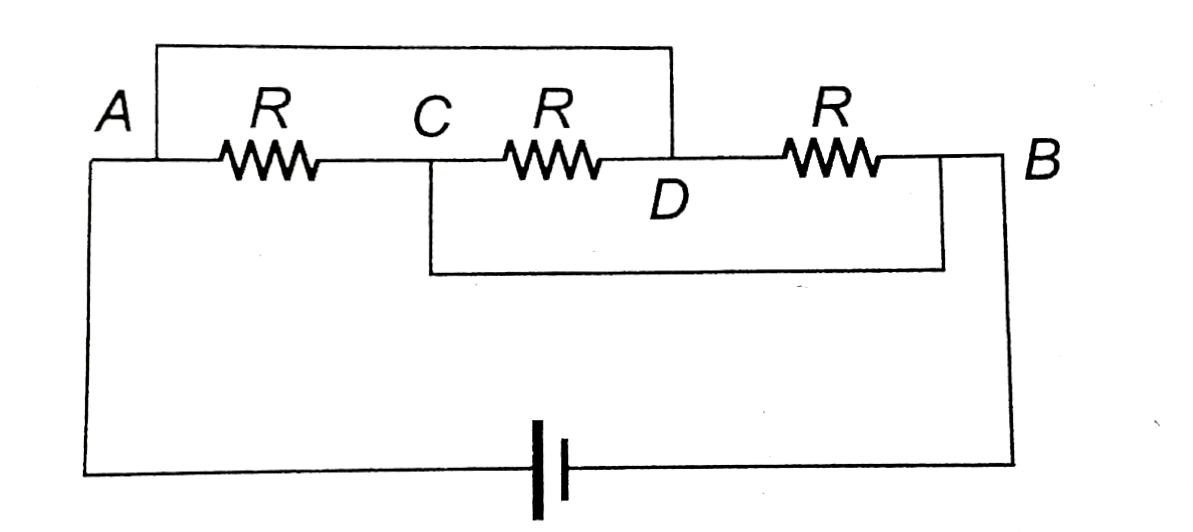
View SolutionThe emf of the cell is 1.8 V and internal resistance is 2/3Ω, calculate the current in the 3Oemga resistance and the power dissipated in the whole circuit.

View SolutionThree batteries of emf E1,E2 and E3 and internal resistance r1,r2 and r3 are connected as shown. The current through the battery of emf E3 is zero if.
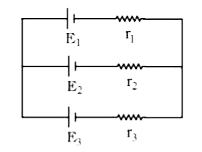
View Solution
