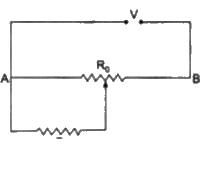
A resistance of R Ω draws current from a potentiometer as shown in the figure. The potentiometer has a total resistance R0Ω. A voltage V is supplied to the potentiometer. Drive an expression for the voltage across R when the sliding contact is in the middle of the potentiometer.

If the sliding contact is in the middle of AC, the wire resistance of AC will be R02 and the circuit can be redrawn as below: Equivalent resistance across AC will be given by
RAC=R02×RR02+R+R02=R0(R0+4R)2(R0+2R)
Current, I=VRAC=2V(R0+2R)R0(R0+4R)
Applying Kirchhoff.s loop law in the loop ABA, we get
−(I−I.)=R02+I.R=0
⇒I.=IR0(R0+2R)
Voltage across resistance R+I.R
=IR0R(R0+2R)=2V(R0+2R)R0(R0+4R)×R0R(R0+2R)
∴VAB=2VRR0+4R

Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (A. MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER)
36 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION FOR COMPETITIVE EXAMINATIONS)
20 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - REVISION EXERCISES (LONG ANSWER QUESTIONS)
10 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A resistance of RΩ draws current from a potentiometer as shown in Fig. The potentiometer has a total resistance R0Ω. A voltage Vis supplied to the potentiometer. Derive an expression for the voltage across R when the sliding contact is in the middle of the potentiometer.

View SolutionA resistance of R draw current from a potentiometer. The potentiometer wire, AB, has total resistance of R0. A voltage V is supplied to the potentiometer. Derive an expression for the voltage across R when the sliding contact is in the middle of potentiometer wire.
View Solution
Knowledge Check
The potentiometer wire of resistance R is connected in series with a cell of e.m.f. E and of resistance Rh. The current flowing through the potentiometer wire is
AI=ER+r+RhBI=ER+rCI=RERh+rDI=ER
A resistance of R draws current from a potentiometer. The potentiometer wire, AB , has a total resistance of R0, A voltage V is supplied to the potentiometer. Derive an expression for the voltage across R when the sliding contact is in the middle of potentialmeter wire.

View SolutionThe given potentiometer has its wire of resistance 10Ω When the sliding contact is in the middle of the potentiometer wire, the potential drop across 2Ω resistor is :
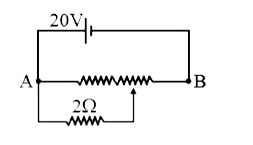
View SolutionA constant voltage of 3 V is supplied to a potentiometer wire. A cell of emf 2 V is balanced by a voltage drop across 416 cm of the wire. Find the total length of the potentiometer wire.
View SolutionThe weight of an object on the surface of the Earth is 40 N. Its weight at a height equal to the radius of the Earth is
View SolutionA current of 1.0 mA is flowing through a potentiometer wire of length 4 m and of resistance 4Ω, find the potential gradient of potentiometer wire
View Solution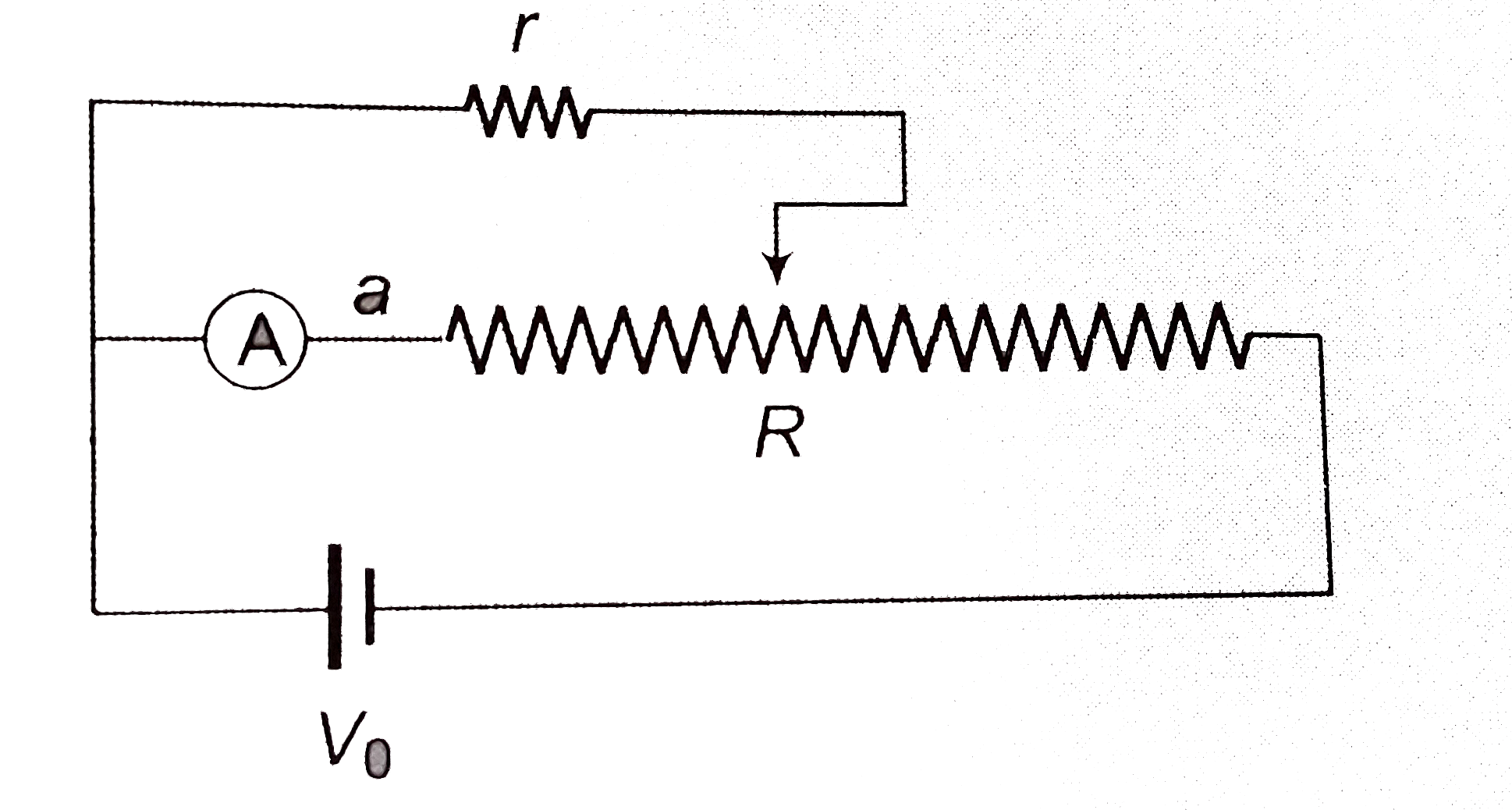
A constant voltage V0 is applied to a potentiometer of resistance R connected to an ammeter. A constant resistor r is connected to the sliding contact of the potentiometer and the fixed end of the potentiometer. How will the reading of ammeter vary as the sliding contact is moved from one end of the potentiometer to the other ? The resistance of ammeter is assumed to be negligible.
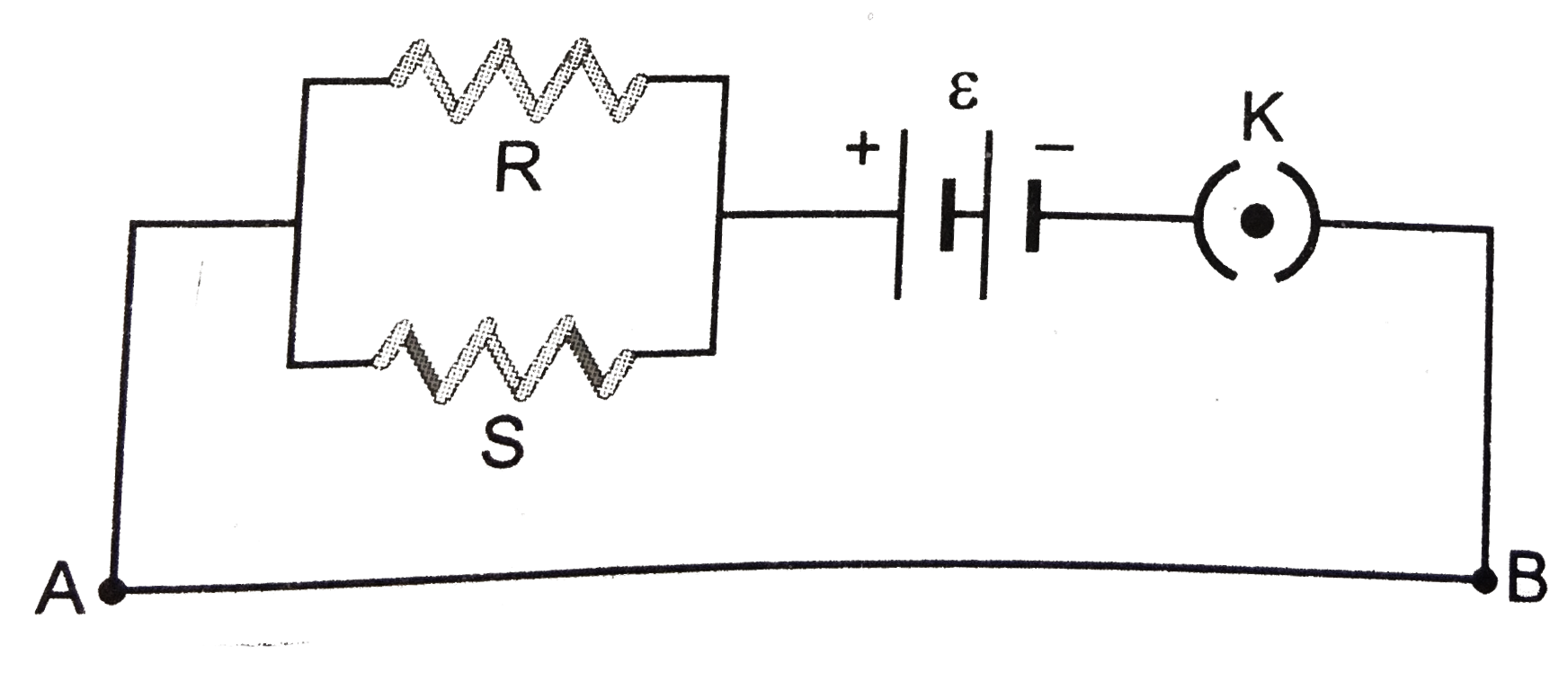
View SolutionA potentiometer wires has a length L and a resistance R0. It is connected to a battery and a parallel resistance combination of R and S as shown in fogure. Find an exprssion for the potential gradient of the potentiometer wire.
View Solution
