The length of a tangent drawn from a point 10 cm away from the centre of the circle of radius 5 cm is
5 cm
cm
cm
cm
The correct Answer is:B
To find the length of the tangent drawn from a point 10 cm away from the center of a circle with a radius of 5 cm, we can use the Pythagorean theorem. Here’s a step-by-step solution:
Step 1: Identify the elements of the problem
- Let O be the center of the circle.
- Let A be the point from which the tangent is drawn, which is 10 cm away from O.
- Let T be the point where the tangent touches the circle.
- The radius OT of the circle is 5 cm.
Step 2: Draw the right triangle
- The triangle OAT is a right triangle where:
- OA is the hypotenuse (10 cm).
- OT is one leg (the radius, which is 5 cm).
- AT is the other leg (the length of the tangent we need to find).
Step 3: Apply the Pythagorean theorem
According to the Pythagorean theorem:
OA2=OT2+AT2
Substituting the known values:
102=52+AT2
Step 4: Calculate the squares
Calculating the squares:
100=25+AT2
Step 5: Rearrange the equation
Now, rearranging the equation to solve for AT²:
AT2=100−25
AT2=75
Step 6: Solve for AT
Taking the square root of both sides:
AT=√75
This can be simplified:
AT=√25×3=5√3 cm
Final Answer
The length of the tangent AT is 5√3 cm.
---
- Let O be the center of the circle.
- Let A be the point from which the tangent is drawn, which is 10 cm away from O.
- Let T be the point where the tangent touches the circle.
- The radius OT of the circle is 5 cm.
- The triangle OAT is a right triangle where:
- OA is the hypotenuse (10 cm).
- OT is one leg (the radius, which is 5 cm).
- AT is the other leg (the length of the tangent we need to find).
According to the Pythagorean theorem:
OA2=OT2+AT2
Substituting the known values:
102=52+AT2
Calculating the squares:
100=25+AT2
Now, rearranging the equation to solve for AT²:
AT2=100−25
AT2=75
Taking the square root of both sides:
AT=√75
This can be simplified:
AT=√25×3=5√3 cm
The length of the tangent AT is 5√3 cm.
Topper's Solved these Questions
- CIRCLES Book:S CHAND IIT JEE FOUNDATIONChapter:CIRCLES Exercise:QUESTION BANK - 38
Explore 1 Video
- CIRCLES Book:S CHAND IIT JEE FOUNDATIONChapter:CIRCLES Exercise:QUESTION BANK - 39
Explore 1 Video
- CIRCLES Book:S CHAND IIT JEE FOUNDATIONChapter:CIRCLES Exercise:QUESTION BANK - 36
Explore 1 Video
- AVERAGEBook:S CHAND IIT JEE FOUNDATIONChapter:AVERAGEExercise:SELF ASSESSMENT SHEET
Explore 10 Videos
- CO-ORDINATE GEOMETRYBook:S CHAND IIT JEE FOUNDATIONChapter:CO-ORDINATE GEOMETRYExercise:Self Assessment Sheet
Explore 10 Videos
Similar Questions
Knowledge Check
The length of the tangent drawn to a circle of radius 4 cm from a point 5 cm away from the centre of the circle is
A3cmB4√2 cmC5√2cmD3√2 cm
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm . Find the radius of the circle.

View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
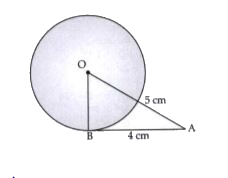
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
View SolutionFind the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
View SolutionThe length of tangent from a point A at a distance of 5 cm from the centre of the circle is 4 cm. What will be the radius of the circle ?
View SolutionThe length of tangent from a point A at a distance of 12 cm from the centre of the circle is 9 cm. What is the radius of the circle ?
View SolutionLength of a tangent drawn to a circle with radius 3 cm from a point 4 cm from the centre of the circle is
View Solution