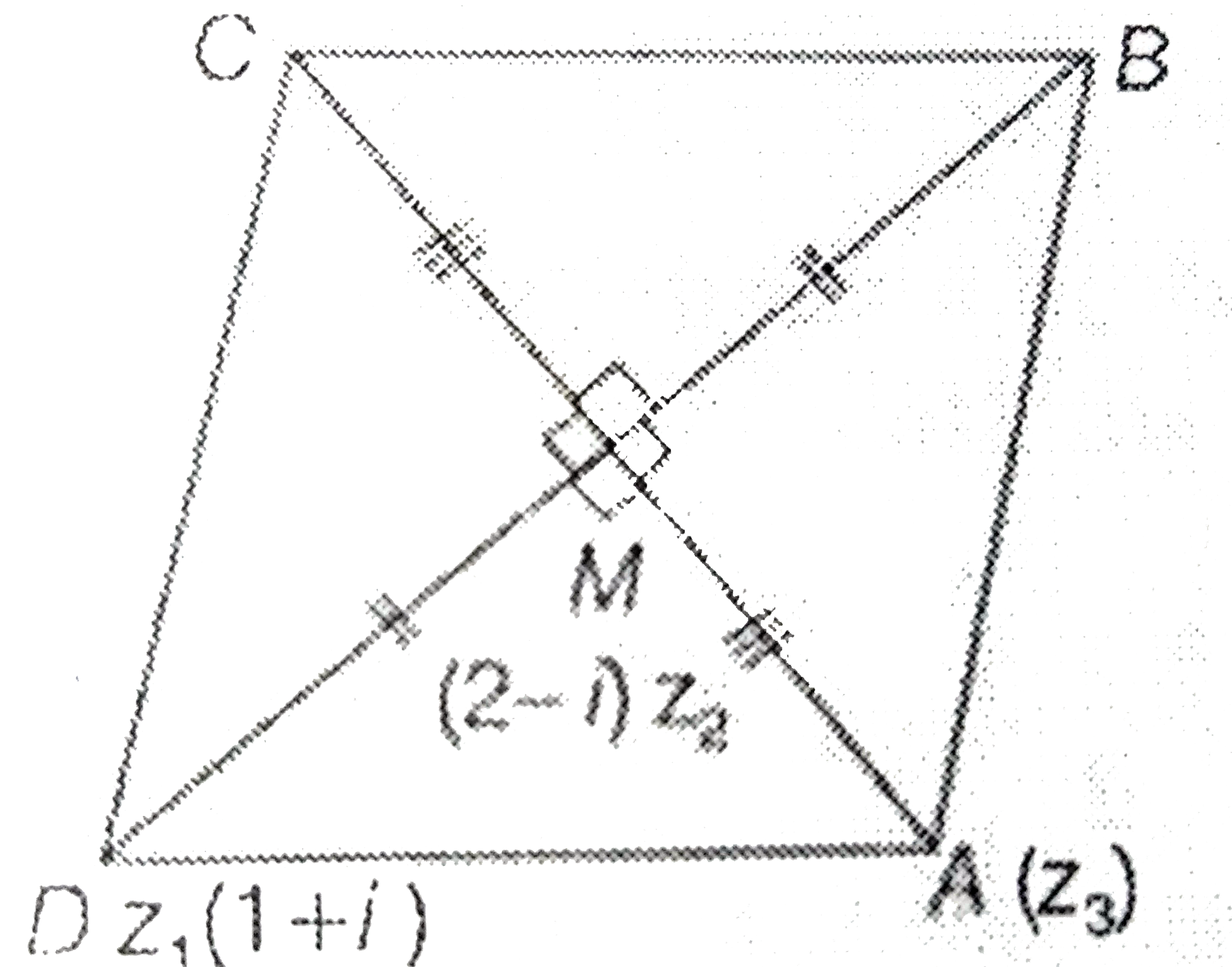
ABCD is a rhombus. Its diagonals $A C and B D$ intersect at the point M and satisfy $B D = 2 A C$ .If he point $D and M$ represent the complex numbers $1 + i and 2 - i$ respectively, then A represents the complex number......or......

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $3 - \frac{i}{2}$ or $1 - \frac{3 i}{2}$

Given D=(1+i),M =(2-i)
and diagonals of a rhombus bisect each other.
Let $B \equiv (a + i b)$ therefore
$\frac{a + 1}{2} = 2, \frac{b + 1}{2} - 1$
$\Rightarrow a + 1 = 4, b + 1 = - 2 \Rightarrow a = 3, b = - 3$
$a + 1 = 4, b + 1 = - 2 \Rightarrow a = 3, b = - 3$
$\Rightarrow B = (3 - 3 i)$

Again $D M = \sqrt{{(2 - 1)}^{2} + {(- 1 - 1)}^{2}} = \sqrt{1 + 4} = \sqrt{5}$
But $B D = 2 D M \Rightarrow B D = 2 \sqrt{5}$
and $2 A C = B D \Rightarrow 2 A C = 2 \sqrt{5}$
$\Rightarrow A C = \sqrt{5} and A C = 2 A M$
$\Rightarrow \sqrt{5} = 2 A M \Rightarrow A M = \frac{\sqrt{5}}{2}$
Now ,let coordinate of A be (x+ iy)
But in a rhombus AD=AB therefore we have
$A D^{2} = A B^{2}$
$\Rightarrow {(x - 1)}^{2} + {(y - 1)}^{2} = {(x - 3)}^{2} + {(y + 3)}^{2}$
$\Rightarrow x^{2} + 1 - 2 x + y^{2} + 1 - 2 y = x^{2} + 9 - 6 x + y^{2} + 9 + 6 y$
$\Rightarrow 4 x - 8 y = 16$
$x - 2 y = 4$
$\Rightarrow x = 2 y + 4$
Again $A M = \frac{\sqrt{5}}{2} \Rightarrow A M^{2} = \frac{5}{4}$
$\Rightarrow {(x - 2)}^{2} + {(y + 1)}^{2} = \frac{5}{4} [from Eq. (i)]$
$\Rightarrow 5 y^{2} + 10 y + 5 = \frac{5}{4}$
$20 y^{4} + 40 y + 15 = 0$
$\Rightarrow 4 y^{2} + 8 y + 3 = 0$
$\Rightarrow (2 y + 1) (2 y + 3) = 0$
$2 y + 1 = 0, 2 y + 3 = 0$
$\Rightarrow y = - \frac{1}{2}, y = - \frac{3}{2}$
on putting these values in Eq.(i) we get
$x = 2 (- \frac{1}{2}) + 4, x = 2 (- \frac{3}{2}) + 4$
$\Rightarrow x = 3, x = 1$
Therefore A is either $(3 - \frac{i}{2}) or (1 - \frac{3 i}{2})$
Alternate Solution
since, M is the centre of rhombus
$∴$ By rotating D about M through an angle of $\pm π / 2$ we get possible position of A .

$\Rightarrow \frac{z_{3} - (2 - i)}{- 1 + 2 i} = \frac{1}{2} (\pm i) \Rightarrow \frac{z_{3} - (2 - i)}{- 1 + 2 i} = \frac{1}{2} (\pm i)$
$\Rightarrow z_{3} = (2 - i) \pm \frac{1}{2} i (2 i - 1) = (2 - 1) \pm \frac{1}{2} (- 2 - 1)$
$= \frac{4 - 2 i - 2 - i}{2}, \frac{4 - 2 i + 2 + i}{2} = 1 - \frac{3}{2} i, 3 - \frac{i}{2}$
$∴ A is either (1 - \frac{3}{2} i) or (3 - \frac{i}{2})$

|

Updated on:21/07/2023

Class 12 MATHS COMPLEX NUMBERS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In a given parallelogram, if the points $P_{1}$ and $P_{2}$ represent two complex numbers $z_{1}$ and $z_{2}$ , then the point $P_{3}$ represents the number
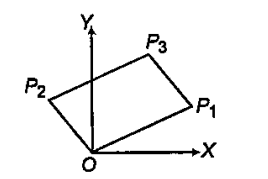A $z_{1} + z_{2}$
B $z_{1} - z_{2}$
C $z_{1} \times z_{2}$
D $z_{1} + z_{2}$
Question 2 - Select One
In a rhombus ABCD the diagonals AC and BD intersect at the point (3,4) . If the point A is (1,2) the diagonal BD has the equation
Ax - y - 1 = 0
Bx + y - 1 = 0
Cx - y + 1 = 0
Dx + y - 7 =0
Question 3 - Select One
The points represented by the complex numbers $1 + i, - 2 + 3 i$ and $\frac{5}{3} i$ on the argand diagram are
AVertices of an equilateral triangle
BVertices of an isosceles triangle
CCollinear
DNone of the above

IIT JEE PREVIOUS YEAR-COMPLEX NUMBERS-TOPIC 4 ROTATION OF A COMPLEX NUMBER (FILL IN THE BLANKS )

Home
Ask Doubt
Profile