Let $T_{1}, T_{2}$ and be two tangents drawn from (-2, 0) onto the circle $C : x^{2} + y^{2} = 1$ . Determine the circles touching C and having $T_{1}, T_{2}$ as their pair of tangents. Further, find the equations of all possible common tangents to these circles when taken two at a time

Video Solution

Text Solution

Verified by Experts

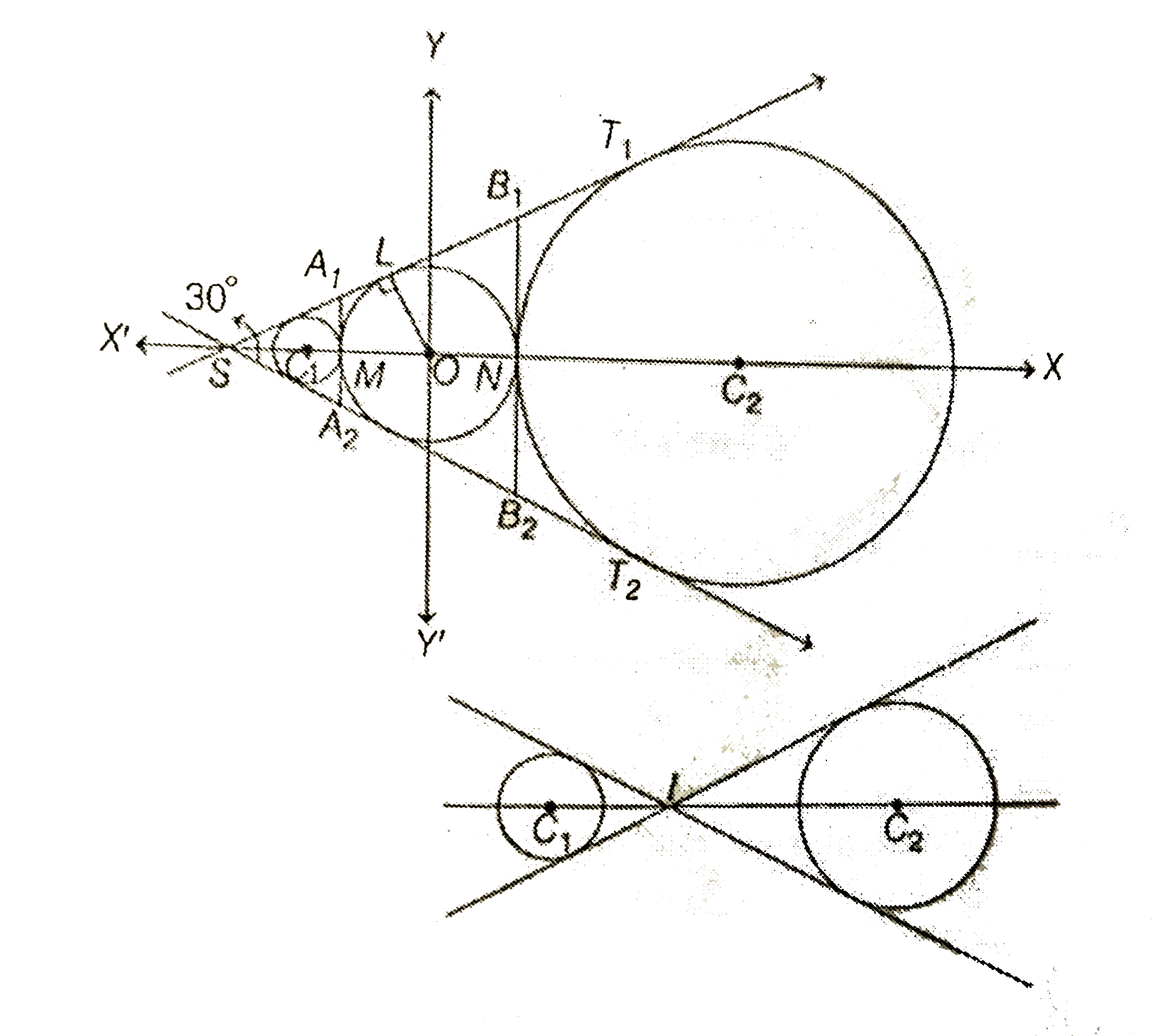
From figure it is clear that, $Δ O L S$ is clear that, $Δ O L S$ is a right triangle with right angle at L.
Also, OL = 1 and OS = 2
$∴ 1 sin (∠ L S O) = \frac{1}{2} \Rightarrow ∠ L S O = 30^{\circ}$
Since, $S A_{1} = S_{2}, Δ S A_{1} A_{2}$ is an equilateral triangle.
the circle with centre at $C_{1}$ is a circle insribed in the $Δ S A_{1} A_{2}$ . Therefore centre $C_{1}$ is a circle inscribed of $Δ S A_{1} A_{2}$ . This $C_{1}$ divides SM in the ratio $2 : 1$ . therefore coordinates of $C_{1}$ are $(- 4 / 3, 0)$ and its radius $= C_{1} M = 1 / 3$
$∴$ Its equation is ${(x + 4 / 3)}^{2} + y^{2} = {(1 / 3)}^{2} ... (i)$
The other cirlce touches the equilateral triangle $S B_{1} A_{2}$ .
externally. Its radius r is given by $r = \frac{Δ}{s - a}$
where $B_{1} B_{2} = a But Δ = \frac{1}{2}) (a) (S N) = \frac{3}{2} a$
and $s - a = \frac{3}{2} a - a = \frac{a}{2}$
Thus, r = 3
$\Rightarrow Coordinates of C_{2} are (4, 0)$ .
$∴$ Equation of circle with centre at $C_{2}$ is
${(x - 4)}^{2} + y^{2} = 3^{2} ... (i i)$
EQuation of common tangents to circle (i) and circle C are
$x = - 1 and y = \pm \frac{1}{\sqrt{3}} (x + 2) [T_{1} and T_{2}]$
Equation of common tangents to circle (ii) and circle C are
$x = 1 and y = \pm \frac{1}{\sqrt{3}} (x + 2) ... [T_{1} and T_{2}]$
Two tangents common to (i) and (ii) ar $T_{1} and T_{2}$ at O. To find the remaining two trasnverse tangents to (i) and (ii), we find a point I which divides the joint of $C_{1} C_{2}$ in the ratio $r_{1} : r_{2} = 1 / 3 : 3 = 1 : 9$
Therefore, coordintates of I are $(- 4 / 5, 0)$
Equation of any line through I is $y = m (x + 4 / 5)$ . It will touch (i) if
$\frac{∣ ∣ m (\frac{- 4}{3} + \frac{4}{5}) - 0 ∣ ∣}{\sqrt{1 + m^{2}}} = \frac{1}{3} \Rightarrow ∣ ∣ ∣ - \frac{8 m}{15} ∣ ∣ ∣ = \frac{1}{3} \sqrt{1 + m^{2}}$
$\Rightarrow 64 m^{2} = 25 (1 + m^{2})$
$\Rightarrow 39 m^{2} = 25 \Rightarrow m = \pm \frac{5}{\sqrt{39}}$
Therefore, these tangents are $y = \pm \frac{5}{\sqrt{39}} (x + \frac{4}{5})$

Updated on:21/07/2023

The equation of pair of tangents to the circle $x^{2} + y^{2} = 16$ drawn from the point (1,4) is
A $x^{2} + y^{2} - x - 4 y = 0$
B $x^{2} + y^{2} + x - 4 y = 0$
C $x^{2} + y^{2} - 2 x - 8 y = 0$
DNone of these
The equation of tangents drawn from the point (0,1) to the circle $x^{2} + y^{2} - 4 x - 2 y + 4 = 0$ are
A2x-y+1=0 ,x+2y-2=0
B2x-y-1=0 ,x+2y-2=0
C2x-y+1=0,x+2y+2=0
D $x = \pm \sqrt{3} (y - 1)$
If two tangents are drawn from a point to the circle $x^{2} + y^{2} = 32$ to the circle $x^{2} + y^{2} = 16$ , then the angle between the tangents is
A $\frac{- π}{4}$
B $\frac{π}{3}$
C $\frac{π}{2}$
D $\frac{π}{6}$